Pour décrire la géométrie de structures tridimensionnelles complexes, le géologue doit pouvoir caractériser l'orientation dans l'espace de surfaces et de lignes, soit à partir de mesures à l'affleurement soit à partir de cartes géologiques.
Orientation d'un plan dans l'espace
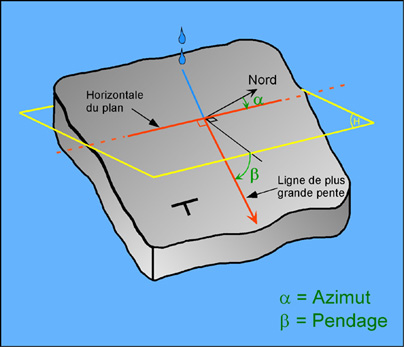
Le plan est la surface géométrique la plus simple. Les surfaces plus complexes peuvent dans tous les cas se résoudre en domaines élémentaires plans. L'orientation d'un plan (ex : stratification, miroir de faille…) nécessite la définition de deux droites remarquables (Fig.1) :
- l' horizontale du plan : elle matérialise sur le plan (P) la trace d'un plan horizontal passant par un point M,
- la ligne de plus grande pente ou ligne de plus grande inclinaison : elle visualise la direction d'écoulement d'un filet d'eau sur le plan (P). Cette ligne est orthogonale à l'horizontale du plan. C'est en fait un axe puisqu'on polarise cette droite selon son plongement.
Donner la géométrie d'orientation d'un plan revient à donner l'orientation de ces deux droites. Pour ce faire, on mesure à l'aide d'une boussole, (1) l'azimut de l'horizontale du plan qui est l'angle entre le Nord géographique et la direction de cette horizontale ; (2) le pendage ou intensité de plongement qui est l'angle entre la ligne de plus grande pente est un plan horizontal (Fig.1). Ce deuxième angle est mesuré avec un clinomètre dont sont munies les boussoles de géologue.
L'orientation d'un plan est notée sous la forme conventionnelle : N45° - 15 SE. Cela revient à dire que son horizontale a un azimut de 45° par rapport au Nord (= direction NW-SE), et que l'intensité de son plongement est de 15° (sous-entendu par rapport à l'horizontale) vers le SE.
Orientation d'une droite dans l'espace
De la même manière, l'orientation d'une ligne dans l'espace nécessite la mesure (1) de sa direction (azimut) c'est à dire l'angle entre le Nord et le plan vertical qui contient la ligne, et (2) de son plongement qui est l'angle entre la ligne descendante et un plan horizontal.
Les isohypses ou horizontales du plan
Les isohypses sont les points d'une surface situés à la même altitude. Les courbes de niveau d'une carte topographique sont les isohypses de cette surface topographique. L'isohypse d'une surface plane est une droite horizontale : elle correspond à l'intersection d'un plan horizontal avec la surface en question. L'ensemble des isohypses d'un plan forme une famille de droites parallèles et équidistantes (Fig.2)
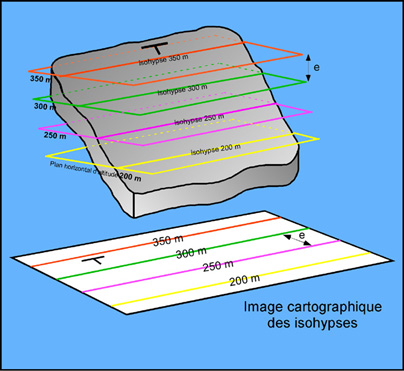
La trace cartographique d'une surface géologique représente l'intersection de cette surface avec la topographie. Les points d'intersection d'une courbe de niveau d'altitude donnée et de la trace cartographique d'un plan sont communs aux deux surfaces. Ils sont donc situés sur l'isohypse de même altitude que celle de la courbe de niveau considérée. L'isohypse étant une droite, ces points s'alignent sur celle-ci. L'opération étant répétée pour différentes courbes de niveau, on construit un ensemble d'isohypses qui caractérisent la surface géologique de la même manière que les courbes de niveau pour une surface topographique (Fig.3)
Lors de la séance de T.T. vous verrez que la construction des isohypses permet de mesurer le pendage d'une strate, son épaisseur, sa trace cartographique.
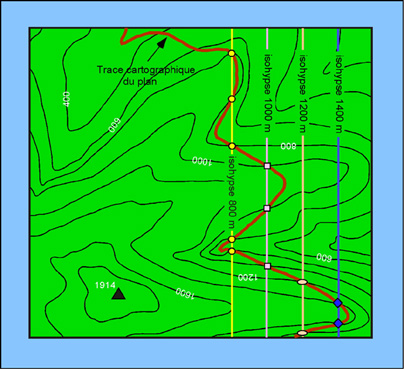
Relations trace cartographique - pendage
Au niveau des vallées la trace cartographique d'un plan marque un V (ou un chevron) dont la pointe est dirigée dans le sens de pendage de la surface. Cette règle est connu sous le nom de " règle des V ". Elle est toujours valable, sauf lorsque le pendage est plus faible que la pente de la vallée. Dans le cas d'un plan horizontal, la trace cartographique est parallèle aux courbes de niveau. A l'inverse, dans le cas d'un plan vertical, la trace cartographique est rectiligne puisque, quelque soit le relief, la projection d'un plan vertical sur le plan horizontal est une droite.