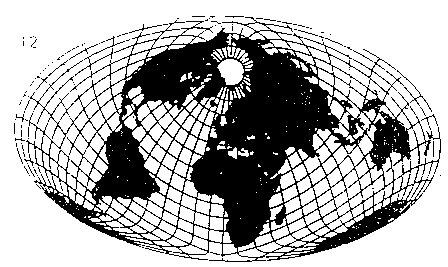
Ces quelques pages ont pour pour but de constituer une petite introduction à la cartographie. Nous aborderons principalement les notions de géodésie et de projection qui sont sous-jacentes à la constitution d'un planisphère.
Après la lecture de ces lignes vous comprendrez pourquoi, alors que des systèmes de positionnement comme le GPS ont une précision de 10 m, on se retrouve avec des erreurs de l'ordre de 200 m par rapport au tracé de la carte scannée qui sert de fond dans des applications de cartographie numérique.
I-La géodésie
La géodésie est la science qui a pour objet l'étude de la forme de la Terre et la mesure de ses dimensions.
Son objectif pratique est la détermination des positions à la surface de la Terre, permettant la localisation pour les travaux de type génie civil, hydrographie, navigation maritime ou aérienne, confection de cartes...
Son objectif scientifique est d'aboutir à la connaissance précise de la forme de la Terre et de son champ de pesanteur. Les implications de ces connaissances sont importantes car elles concernent l'ensemble des sciences de la Terre.
A-La forme de la Terre
Le phénomène physique qui régit la forme de la Terre est la pesanteur. Cette force résulte des forces de gravitation dues à la masse de la Terre et de la force centrifuge liée à la rotation de la Terre.
On sait, depuis l'Antiquité que la forme de la Terre est sensiblement sphérique. Jusqu'au XVIIeme siecle, la valeur admise pour le rayon terrestre était R = 6 372 km
Peu après Newton et Huyghens déduisent de considérations théoriques sur la rotation de la Terre que celle-ci doit avoir une forme d'ellipsoide de révolution aplati aux pôles.
La deuxième moitié du XVIIIeme et une grande partie du XIXeme seront consacrées à la recherche des paramètres de cet ellipsoide.
Les valeurs actuellement admises sont:
- demi grand axe : a=6 738 137 m,
- demi petit axe : b=6 356 752.3 m,
- aplatissement : f=1 / 298.257.
Toutefois, l'assimilation de la Terre à une sphère reste possible pour des cartes à très petite échelle (<1/5000000). En effet, à ces échelles la différence entre une sphère et un ellipsoide est indétectable.

B-Le Géoide
On démontre que la pesanteur dérive d'un potentiel appelé potentiel terrestre. Il existe une infinité de surfaces équipotentielles dites surfaces de niveau sur lesquelles le potentiel est constant. Ces surfaces sont en chacun de leur points perpendiculaires à la verticale.
Le niveau moyen des mers n'est pas rigoureusement une surface équipotentielle (en raison de la différence de densité des eaux et des courants permanents) mais on peut la considérer comme telle avec une approximation de l'ordre du mètre. La surface coincidant avec le niveau moyen des mers est appelé le Géoide.
Un point se promenant sur cette surface ne monte ni ne descend. Le Géoide est la surface de référence des altitudes.
C-Coordonnées géocentriques
On peut donc assimiler la Terre à un solide indéformable et choisir un repère Txyz lié à ce solide.
- T : Centre d'inertie de la Terre,
- Tz : axe de rotation de la Terre,
- Txy : plan du premier mé:ridien, contenant Tz et un point particulier de l'observatoire de Greenwich (UK).
Le mouvement de Txyz par rapport aux étoiles est déduit des lois de la mécanique.
Un point M de la surface de la Terre est repéré par ses coordonnées cartésiennes (x, y, z) .
Si l'équation de la surface est définie, alors les coordonnées cartésiennes dépendent de la latitude et de la longitude géocentrique du point.
D-Les surfaces de référence
Ces deux coordonnées (lati, longi) permmettent en théorie d'identifier un point quelconque de la Terre. Cependant, le rayon TM n'est pas définissable mathématiquement du fait du relief.
Compte tenu des faibles variations de cette distance, il est commode d'introduire une surface de référence, généralement un ellipsoide, qu'il suffira de coiffer du relief approprié pour représenter la surface de la Terre.
Le Géoide et un ellipsoide de référence étant définis, on leur associe en un point M quelconque deux directions :
- La verticale physique, assimilée à une droite perpendiculaire au Géoide (Vecteur V).
- La normale à l'ellipsoide de référence (Vecteur V').
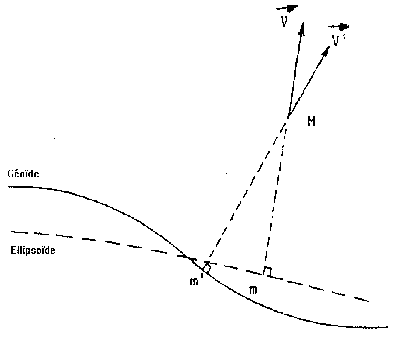
L'angle entre ces deux directions est la déviation de la verticale qui dépend du choix de l'ellipsoide de référence mais doit être inférieur à 20" pour un ellipsoide bien choisi.
E-Altitude
L'altitude zéro est fixée au Géoide. On appelle altitude orthométrique du point M la distance verticale séparant ce point du Géoide. Malheureusement, cette quantité n'est ni observable directement ni calculable exactement car le Géoide n'est pas parfaitement connu sous les continents.
Pour les besoins des scientifiques, les géodésiens définissent une altitude conventionnelle liée à la différence de potentiel terrestre entre un point et le Géoide.
L'altitude ellipsoidique est facile à définir pour un ellipsoide de référence donné. C'est la distance entre ce point et l'ellipsoide en suivant la normale.
F-Système géodésique
Le choix des dimensions de l'ellipsoide de référence ne suffit pas à définir un repère.
Il faut aussi fixer sa position par rapport à la Terre.
La position de l'ellipsoide est définie en imposant l'égalité des coordonnées astronomiques et géodésique en un point dit point fondamental et en fixant l'altitude de ce point.
Un système géodésique est matérialisé par un ensemble de points dont les coordonnées sont déterminées dans le système considéré.
Les coordonnées d'un point quelconque sont établies par mesure d'angles et de distances avec les points géodésiques voisins.
L'ensemble des points géodésiques constitue ce que l'on appelle le réseau géodésique du système.
La méthode traditionnelle de construction d'un réseau géodésique à partir de point fondamental est la triangulation. Les points géodésiques sont placés aux sommets d'un assemblage de triangles sensiblements équilatéraux dont on mesure les angles sur le terrain.
G- Coordonnées astronomiques.
La latitude astronomique est l'angle que fait la verticale passant par le point à situer avec l'équateur. Elle est exprimée en degrés de -90 (pôle Sud) à +90 (pôle Nord).
La longitude astronnomique est l'angle entre le méridien du point et le premier méridien. Un méridien est défini comme le plan caractérisé par la verticale et la parallèle à la ligne des pôles passant par le point. Elle varie entre -180 et +180 de part et d'autre du méridien de référence, les négatifs allant vers l'Ouest et les positifs vers l'Est.
H-Coordonnées géodésiques
Les coordonnées géodésiques sont définies par analogie avec les coordonnées astronomiques en substituant la verticale par la normale.
I-Coordonnées horizontales
Si on choisit un point de référence sur le géoide et que l'on se place dans le plan perpendicluaire à la verticale en ce point, on définit un nouveau repère dit "repère astronomique local".
Dans ce repère, un point est localisé par son azimut et son zénith. L'azimut est l'angle entre la droite reliant le point au point de référence et la droite définie par l'intersection du plan horizontal avec le méridien du point de référence, il va de 0 à 360 degrés dans le sens rétrograde (du Nord vers l'Est). Le zénith est défini comme l'angle entre la verticale et la droite reliant le point à situer avec le point de référence, il est compté de 0 à 180 degrés. L'angle complémentaire au zénith est la hauteur.
II-Les projections
L'application d'une surface plane sur une sphère est impossible sans pliage ou déchirure, et la représentation plane d'une surface sphérique conduira toujours à des déformations de la disposition relative des points de cette surface. Cette déformation peut etre source d'erreurs dans l'interprétation d'images géographiques et il est bon d'en etre prévenu et de connaitre les principes des chopix de projections en fonction de l'utilisation.
A-La déformation
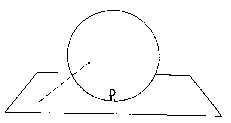
Soit un plan tangent en un point P à une sphère. Hors de ce point, tout cercle de très petite dimension sur la sphère :
- peut etre représenté sur le plan par un cercle, mais de surface plus grande. Un tel système est dit conforme. En un point de la carte, les angles seront semblables à leurs correspondant sur la sphère. Cependant, les déformations sur cette sphère sont considérables.
- peut etre représenté par une surface équivalente mais de forme elliptique. Un tel système est dit équivalent. Les déformations d'angles sont considérables mais toute surface du plan est équivalente à la surface sphérique correspondante.
Tout cercle de grande dimmension sur la sphère, hors ceux centrés sur P, sera déformé sur le plan.
Il existe des systèmes, dit systèmes compensés ou aphylactique, qui établissent une balance entre les déformations d'angles et les déformations de surfaces.
Dans tous les cas, dès que l'on envisage de représenter une partie notable de la Terre, il y a toujours une déformation des directions et des distances, hors de celles définies à partir de P.
B-Point de vue
En se déplaçant, le point de vue peut prendre des positions remarquables et définir des systèmes intéressants.
- Placé au centre du globe, le point de vue définit la projection gnomonique dans laquelle tout arc de cercle est représenté par une droite.
- Placé sur le globle, il définit la projection stéréographique, qui est conforme.
- Quand le point de vue est extérieur au globe, les perspectives deviennent naturelles, "photographiques".
- Rejté à l'infini, la perspective est othogonale.
- Pour dépasser la demi sphère, le globe peut etre considéré comme transparent et le point de vue placé au coté opposé à la région à représenter.
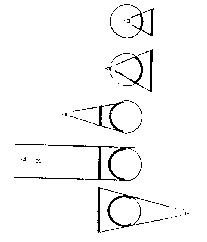
C-Plan de projection
Placer le plan de projection tangent à la sphère n'est pas toujours la meilleur solution.
Si la région à représenter est allongée, on profitera de ce que le plan peut, sans déchirure en cylindre ou en cone. Le point P devient une ligne le long de laquelle il n'y pas de déformation.
Une région inscriptible dans un carré ou un cercle sera représentée dans un système azimutal, c'est à dire construit sur le principe du point tangent.
Lorsque la ligne d'interet est un arc de cercle, les systèmes cylindriques sont les mieux adaptés.
Lorsque la ligne d'interet se rapproche d'un petit cercle, les sytemes coniques sont généralement retenus.
La tangence peut faire place à la séquence et fournir deux lignes de contact.
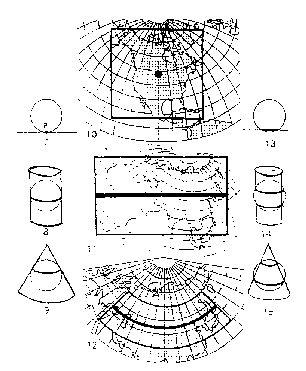
D-Région favorisée
Les déformations diverses s'accentuent du lieu central vers les bords. La figure ci-dessous donne la cartographie des déformations dans le cas de deux projections différentes
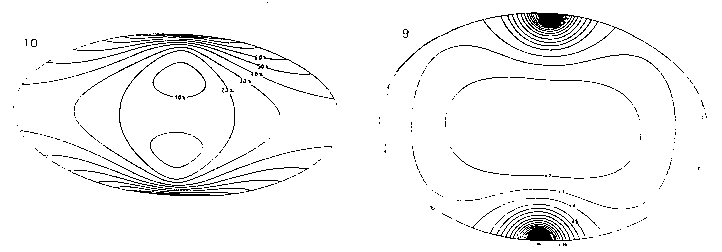
Il est donc normal de chercher à faire coincider le point inévitable de déformation maximale avec la situation géographique la moins genante. ainsi on souvent chercher à placer les continents dans la zone de moindre déformation et à profiter de l'immense vide de l'Océan Pacifique.
Il en résulte deux grandes familles de planisphères :
Les planisphères classiques, où l'on fait coincider les axes mathématiques de la projection avec le système géographique des coordonnées.
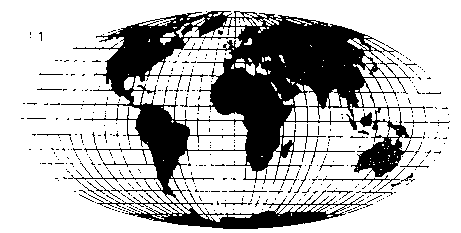
Les planisphères de deuxième générations, utilisant des projections dites obliques et cherchant à faire correspondre les zones de moindre déformation avec le maximum de régions continentales.