Coursgeologie.com

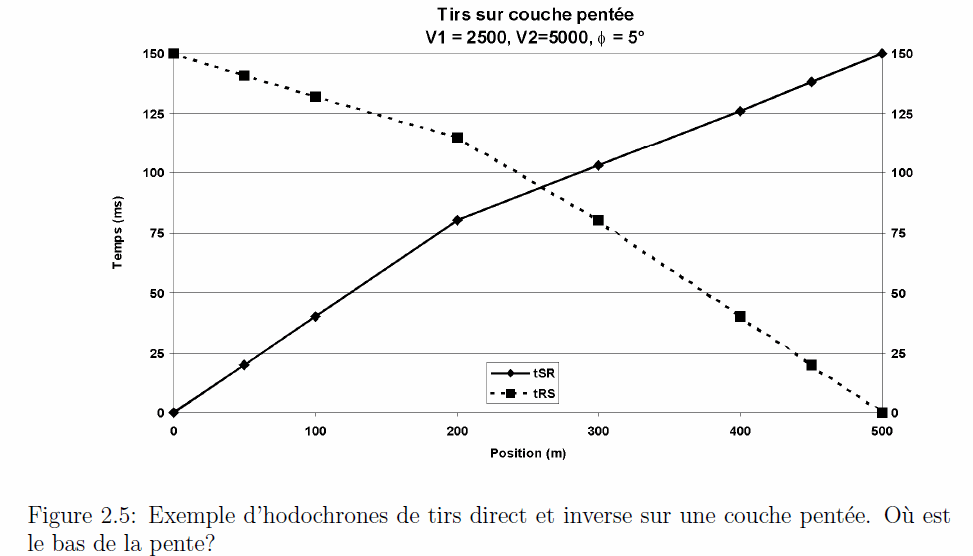
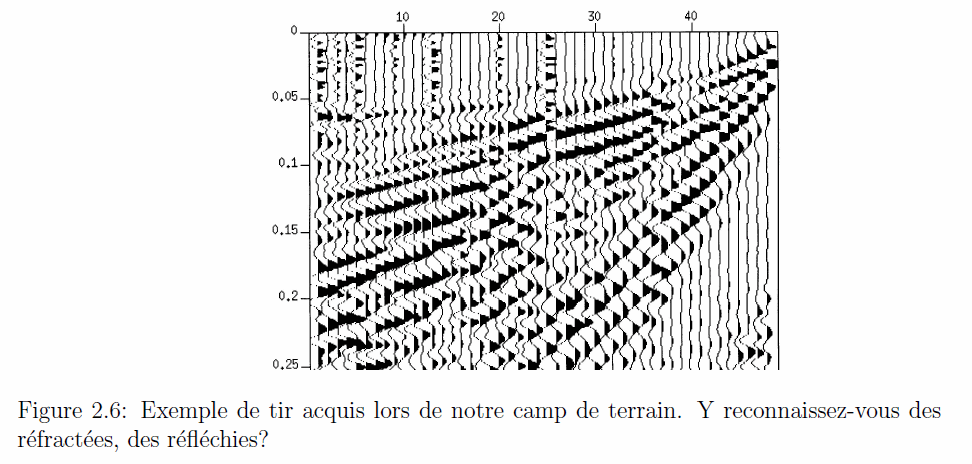
La prospection sismique est basée sur la propagation des ondes élastiques dans le sous-sol. Nous avons indiqué dans la section précédente que l’on s’intéressait essentiellement aux ondes de volume, à savoir les ondes de dilatation-compression (ondes P) et de cisaillement (ondes S).

Vous avez vu lors de notre sortie de terrain comment on met en oeuvre la prospection sismique. On provoque un impact avec une source (e.g. un fusil ou un coup de masse) et les ondes sismiques qui sont générées par la source se propagent dans le sous-sol. Lorsqu’elles arrivent sur un interface entre deux couches de vitesses différentes, une partie des ondes sont réfléchies vers la surface, l’autre partie étant transmise dans les couches plus profondes.

Les angles d’incidence, de réflexion et de transmission sont reliés par le paramàtre de rai, p, qui est constant pour chaque rayon

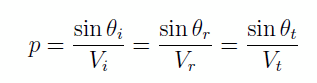
ou θi,r,t et Vi,r,t  sont les angles et les vitesses dans les milieux incident, réfléchi et réfracté.

Nous nous intéresserons ici dans un premier temps aux ondes réfléchies, puis aux ondes transmises.

Soit une onde sismique émanant d’une source S et incidente sur un interface entre deux milieux de vitesses constantes V 1 et V 2. La couche de vitesse V 1 a une épaisseur h. L’onde réfléchie est enregistrée par un récepteur (i.e. un géophone ou un hydrophone) à une distance x de la source (cf. Figure 2.1).

Nous allons résoudre ce problàme en se basant sur la théorie des rais, ce qui a pour avantage de ramener ces problàmes à de simples questions de géométrie. Notez que les rais n’ont pas d’existence physique: ce n’est pas le passage d’un rai qu’on enregistre avec un géophone, mais bien celui d’un front d’onde. On peut bien sˆr résoudre ces problàmes en faisant appel à des fronts d’onde, mais le formalisme est plus compliqué.

Nous allons chercher à calculer le temps de parcours aller-retour entre la source et le récepteur. Pour ce faire, comme la vitesse est constante dans la couche, on n’a qu’à prendre

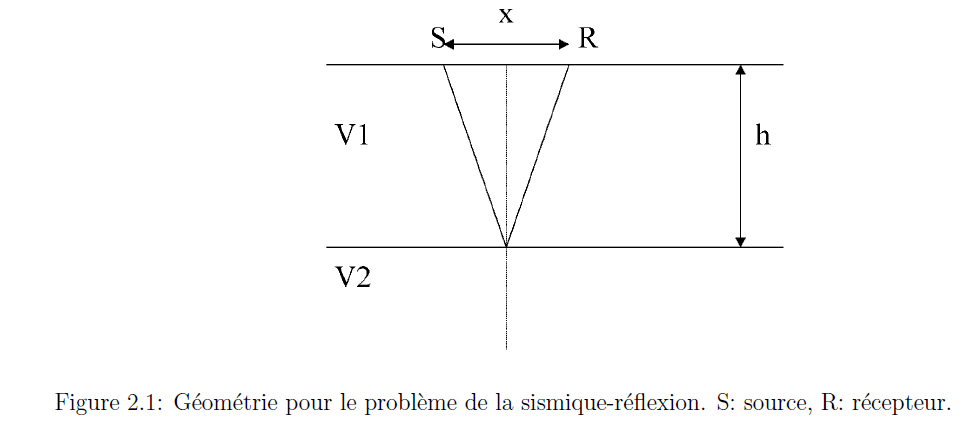
la distance parcourue que l’on divise par la vitesse. Suivant la Figure 2.1, on trouve que cette distance est donnée par

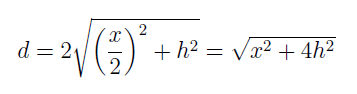
donc le temps de parcours est

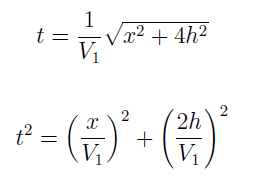
Cette courbe décrivant la relation entre le temps de parcours et la distance source- récepteur est connue sous le nom d’hodochrone. L’hodochrone caractéristique d’une onde réfléchie est une hyperbole, i.e. si vous apercevez une hyperbole sur un tir sismique, vous avez affaire à une onde réfléchie.

On remarque que seul le premier terme dépend de la distance x. Le second terme ne dépend que des paramàtres de la couche: il s’agit en fait du temps aller-retour entre la surface et le bas de la couche défini par t0 = 2h/V1. Notre hodochrone devient donc:

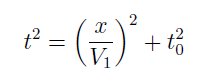
Le cas d’une couche plane est relativement simple. Que se passe-t-il si on est en présence d’une une couche pentée? La géométrie du problàme est présentée sur la Figure 2.2. On remarque que dans ce cas le point de réflexion (Q) n’est pas exactement à mi-chemin entre la source et le récepteur.

Pour résoudre ce probléme, on procàde comme dans le cas précédent, c’est-à-dire qu’on détermine la distance parcourue que l’on divise par la vitesse du milieu. Pour se faciliter les

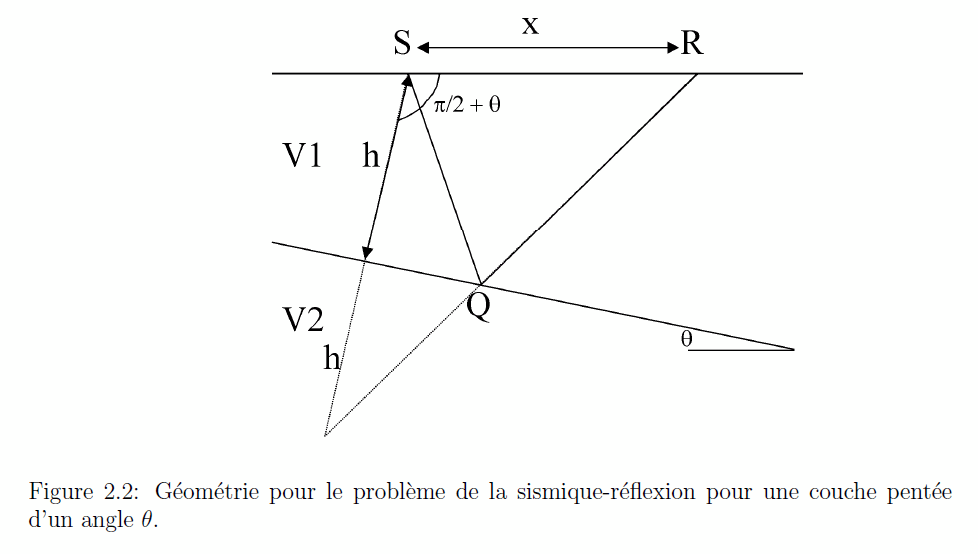
choses, on tourne le parcours SQ par rapport au plan réflecteur: le trajet total est alors du croisement des deux lignes pointillées (P) au point R.

On trouve cette distance PR en applicant la Loi des Cosinus, car le triangle SPR ne contient pas d’angle droit.

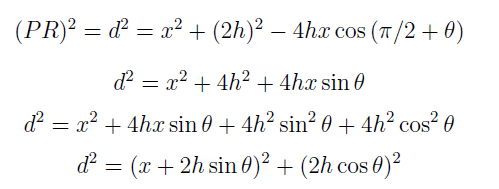
d’ou on tire le temps de parcours

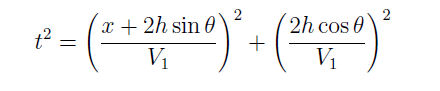
On voit que l’hodochrone décrit encore une hyperbole. Regardons le second terme: comme dans le cas précédent, il ne dépend pas de x. On voit qu’en fait ce terme n’est autre que le t0 du cas précédent divisé par cos θ; autrement dit, il s’agit du t0 pour une vitesse de propagation Vv = V1/ cos θ. Vv  est la vitesse apparente verticale plus élevée que V1.

L’analyse d’une hodochrone nous donne donc des informations sur la vitesse de la couche (qui contrˆle sa courbure) et sur son épaisseur. Mais nous avons vu lors du camp de terrain que les signaux sismiques étaient de plus ou moins grande amplitude. Peut-on utiliser celle-ci pour en savoir un peu plus?

L’amplitude d’une onde réfléchie dépend essentiellement du contraste d’impédance en- tre les deux milieux. L’impédance est définie comme le produit de la vitesse et de la densité Z = ρV . Le coefficient de réflexion R, pour une onde incidente normalement sur un interface est donné par

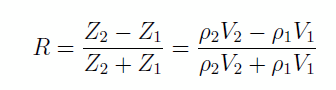
donc, plus la différence entre deux milieux est grande, plus R sera important. Notez aussi que R est positif d’un milieu lent vers un milieu rapide et vice-versa.

Regardons maintenant ce qui se passe dans la couche de vitesse V2 Nous avons vu plus haut que le paramàtre de rai p est constant. Donc, la trajectoire du rai dans le milieu 2 est donnée par

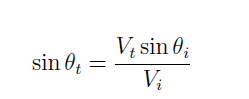
On voit donc que si Vt > Vi, le rai sera plus éloigné de la normale dans le milieu 2 que dans le milieu 1. On peut même imaginer un cas pour lequel sin θt = 1, soit θt = π/2. Ce cas se produira quand

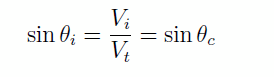
ou θc est l’angle critique, c’est-à-dire l’angle pour lequel le rai se propage le long de l’interface dans le milieu 2. On parle d’onde réfractée critiquement ou d’onde conique.

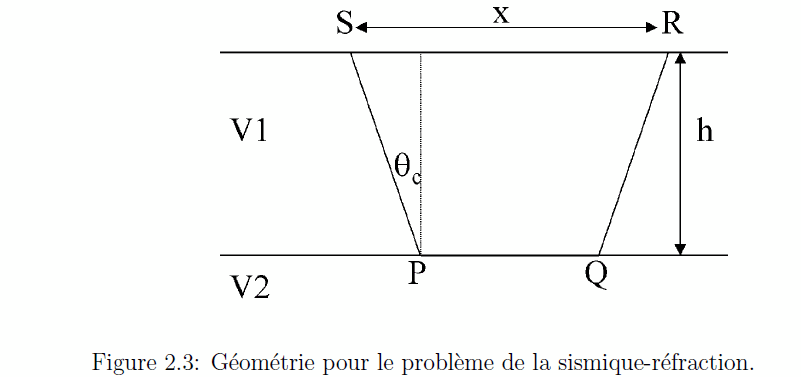
Nous allons calculer l’hodochrone pour une onde conique se propageant le long d’un interface plan (cf. Figure 2.3). Notre approche sera de ”diviser pour régner”, i.e. nous regarderons les trajets dans les couches 1 et 2 séparément.

Dans la couche 1, le trajet est

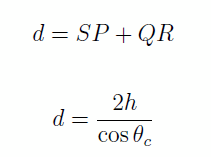
donc le temps de parcours est

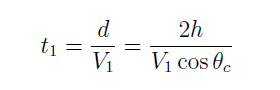
Dans la couche 2, le trajet est

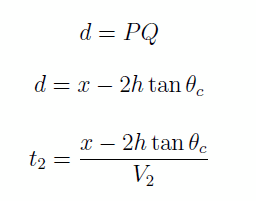
Combinons les deux temps pour trouver le temps total t

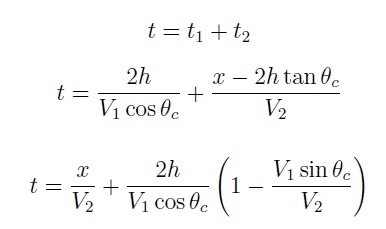
mais V1/V2 = sin θc, , d’ou

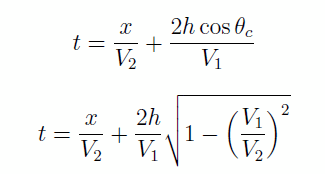
On voit qu’ici, l’hodochrone est une simple droite de pente 1/V2 et dont l’ordonnée à l’origine ne dépend que de l’épaisseur de la couche et des vitesses de part et d’autre de l’interface.

Nous pouvons généraliser cette relation pour un milieu à N vitesses (on ne fera pas la démonstration ici):

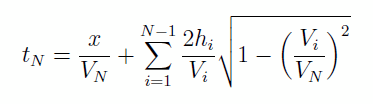
ou tN est l’onde conique se propageant à l’interface au-dessus de la couche N , i.e. l’interface le plus profond. Si on s’intéresse à un interface moins profond, on n’a qu’à choisir un N immédiatement supérieur à l’interface désirée.

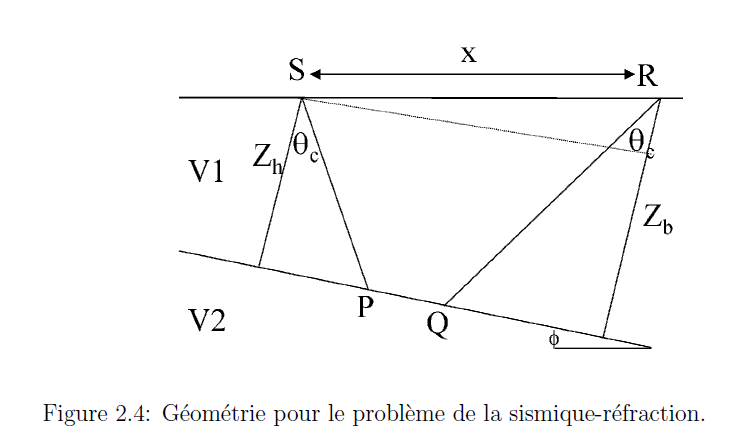
Comme pour le cas de la réflexion, il est souhaitable de calculer l’hodochrone pour un interface penté. La géométrie de ce problàme est donnée dans la Figure 2.4.

Comme dans le cas précédent, divisons pour régner. Le temps de parcours total est la somme des temps dans chaque milieu. Selon la Figure 2.4,

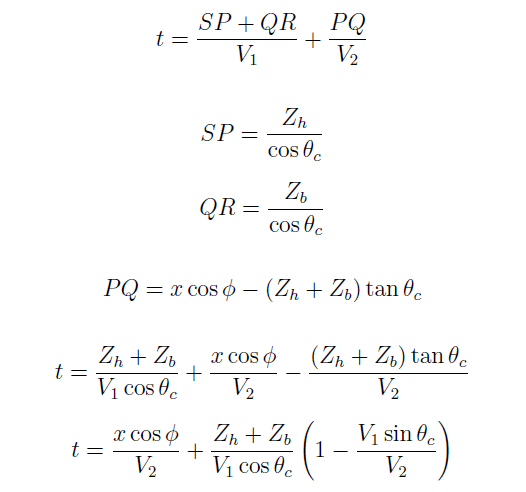
mais V1/V2 = sin θc,, d’ou

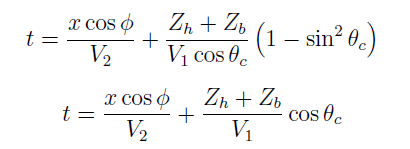
Nous voici donc confrontés à deux cas de figure: soit le tir est réalisé de S vers R (tir direct) ou de R vers S (tir inverse). Déterminons les hodochrones pour ces deux cas.

i. Tir en S. On tire alors vers le bas de la pente. Comme on sait que Zh et Zb sont reliés par x et φ, on va éliminer Zb en utilisant la relation Zb = Zh + x sin φ

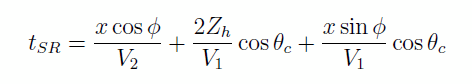
mais sin θc = V1/V2 donc

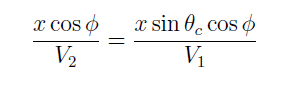
substituons

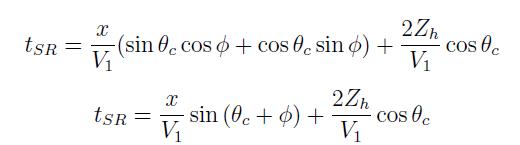
ii. Tir en R. On tire alors vers le haut de la pente. On élimine Zh en utilisant la relation Zh = Zb − x sin φ. En suivant le même raisonnement, on retouve

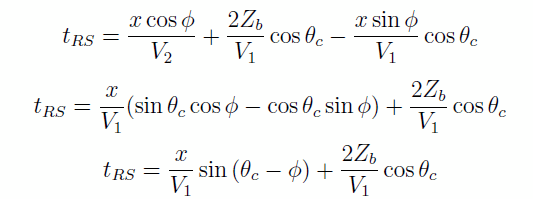
Dans les deux cas, on remarque que l’hodochrone est une droite, mais les pentes (i.e. les vitesses) sont différentes

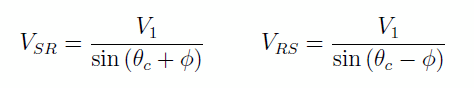
Ces vitesses apparentes nous permettent de déterminer, sans aucun calcul, oà sont le haut et le bas de la pente de l’interface. En effet, comme θc et φ sont des nombre positifs, on sait que θc + φ > θc − φ et donc que VSR < VRS . Le tir à la vitesse apparente la plus élevée est au-dessus du bas de la pente. Mais on peut aller plus loin et déterminer les deux angles θc et φ à partir de ces vitesses apparentes

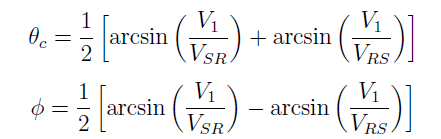
d’ou on tire ensuite V2, Zh et Zb..

On voit donc l’importance d’effectuer au moins un tir direct et un tir inverse afin de déterminer le pendage. Si on n’a qu’un seul tir à notre disposition, on est obligé d’interpréter nos données de sismique-réfraction en termes de couches planes.