Coursgeologie.com

La matière cristallisée présente dans sa structure et dans toutes ses propriétés des caractères de symétrie. De manière interne, un cristal, et donc un minéral, est constitué d'un agencement tridimensionnel de particules (atomes, ions, molécules) selon un modèle régulier : le réseau cristallin. La forme régulière externe est une conséquence de l'agencement régulier de ces particules.

Les formes des cristaux ne sont pas quelconques. Dans les collections de minéraux, il existe des très belles pièces avec des formes très bien développées (prismes de quartz, cubes de pyrite, rhomboèdres de calcite). L'existence de ces formes est liée au fait que dans certains cas, les minéraux ont suffisamment d'espace autour d'eux pour croître et prendre des formes qui leur sont propres. Ces formes macroscopiques traduisent le fait que les atomes sont arrangés à l'échelle microscopique.

Une figure est dite "symétrique" si l'on peut trouver une opération qui laisse cette figure invariante. Alors, la figure originale et la figure résultant de l'opération coïncident totalement. Ces opérations sont appelées opérations de symétrie. Les points, droites et plans par rapport auxquels les opérations sont réalisées, sont appelés éléments de symétrie.

Une opération de symétrie chez les cristaux est donc une opération géométrique qui amène en correspondance des sommets, des arêtes ou des faces d’un cristal.

Les opérations de symétries sont :

• La rotation
• La réflexion
• L’inversion
• La rotoinversion

Les éléments de symétrie correspondants sont dans l’ordre :

• Axes de symétrie simple
• Plan de symétrie
• Centre de symétrie
• Axes de symétrie inverse ou axes d’inversion

Imaginons un petit cristal en deux dimensions composé d’atomes disposés suivant un arrangement ordonné comme cela est montré dans la figure ci-dessous. Bien que tous les atomes dans le réseau soient les mêmes, nous avons coloré l’un d’eux en gris pour pouvoir suivre sa position.

Lorsque nous tournons le cristal d’un angle de 90°, nous remarquons que le réseau et le cristal montrent exactement la même figure précédente. Si nous le tournons à nouveau d’un angle de 90° nous observerons la même chose. Encore une rotation de 90° et on obtient un cristal identique aux précédents. Enfin, une autre rotation de 90° ramène le cristal à son orientation primitive. Ainsi, au cours d’une rotation de 360°, le cristal s’est répété 4 fois. On dit que cet objet possède une symétrie de rotation d’ordre 4. Cette rotation s’est effectuée autour d’un axe perpendiculaire au centre de l’objet.

L’axe autour duquel la rotation de l’objet s’est effectuée est un élément de symétrie connu sous le nom d’axe de rotation ou de symétrie.

Un axe de symétrie est donc une droite imaginaire à partir de laquelle un cristal tournant sur lui-même présente la même image 1 ou plusieurs fois au cours d’une rotation de 360°. Les principaux axes de symétrie possible dans les cristaux sont les suivants :

a. Axe de symétrie d’ordre 1

Un objet qui doit effectuer une rotation de 360° pour retrouver son aspect initial ne possède pas une symétrie de rotation. Puisqu’il se répète une seule fois tous les 360° on dit qu’il possède un axe de symétrie d’ordre 1. Symbole : A1

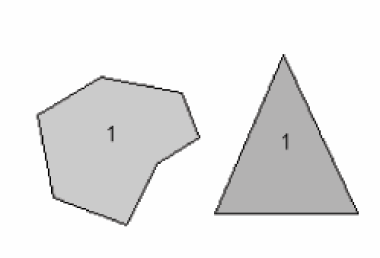
b. Axe de symétrie d’ordre 2

Si un objet est identique à lui- même après une rotation de 180°, c'est-à- dire qu’il se répète 2 fois au cours d’une rotation de 360°, on dit alors qu’il possède un axe de symétrie d’ordre 2 (360/180 = 2). Symbole : A2 ou 2. Une ellipse remplie est utilisé comme symbole pour localiser la trace de l’axe de symétrie d’ordre 3 sur les figures.

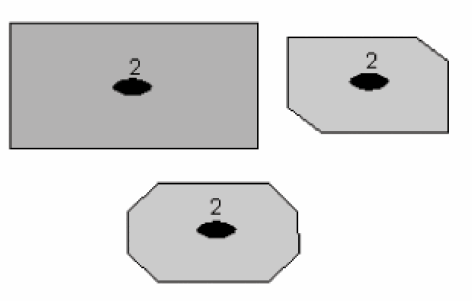
c. Axe de symétrie d’ordre 3

Les objets qui se répètent 3 fois au cours d’une rotation de 360°, et donc chaque 120° possèdent un axe de symétrie d’ordre 3 (360/120 = 3). Symbole : A3 ou 3. Un triangle rempli est utilisé comme symbole pour localiser la trace de l’axe de symétrie d’ordre 3 sur les figures.

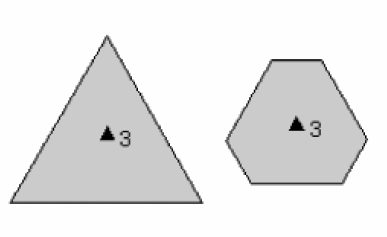
d. Axe de symétrie d’ordre 4

Un objet possède un axe de symétrie d’ordre 4 si il est identique à lui même après une rotation de 90° (et donc 4 fois au cours d’une rotation de 360°). Symbole : A4 ou 4. Un carré rempli est utilisé comme symbole pour localiser la trace de cet axe sur les figures.

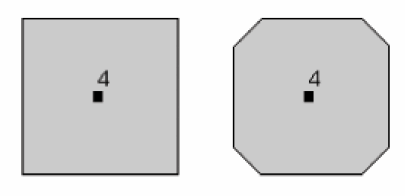
e. Axe de symétrie d’ordre 6

Un objet possède un axe de symétrie d’ordre 6 si il est identique à lui même après une rotation de 60° (360/60 = 6). Symbole : A6 ou 6. Le symbole de cet axe sur les figures est un hexagone rempli.

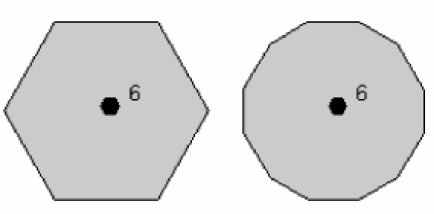
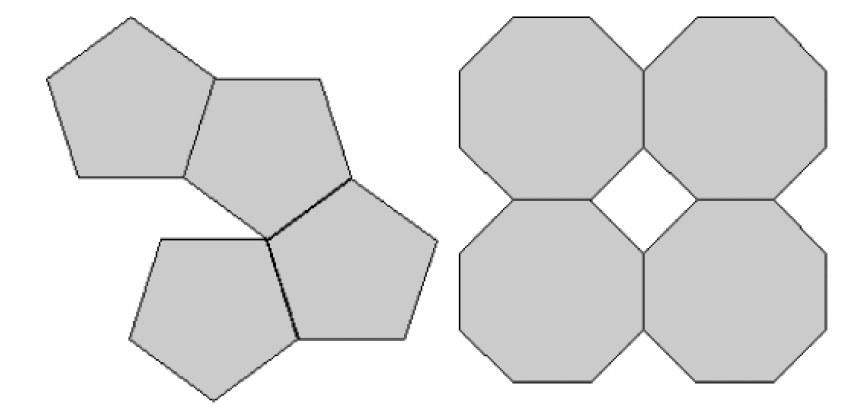
Bien que des objets puisses posséder des axes de symétrie d’ordre 5, 7, 8 ou plus, ceci n’est pas possible pour les cristaux. La raison est que la forme externe d'un cristal est basée sur un arrangement géométrique d'atomes. Si nous essayons de combiner des objets avec des axes de symétrie d’ordre 5 ou 8, nous ne pouvons pas les combiner de telle façon à remplir complètement l’espace, comme cela est illustré ci-dessous.

Un cristal peut être symétrique par rapport à un plan (réflexion), de telle manière que s'il était coupé en deux par ce plan, une moitié serait l'image de l'autre comme dans un miroir. Un plan de symétrie est un plan imaginaire où tous les sommets d’un cristal se correspondent deux à deux sur des droites perpendiculaires et équidistantes par rapport à ce plan. Le symbole d’un plan de symétrie est m.

Les rectangles de la figure suivante possèdent deux plans de symétrie (ou miroirs). Le rectangle de gauche montre le plan de symétrie qui parcourt verticalement la page. Le rectangle à droite montre le plan de symétrie qui parcourt horizontalement la page. Les parties en pointillés des rectangles du bas montrent les parties qui seraient réfléchies par les miroirs.

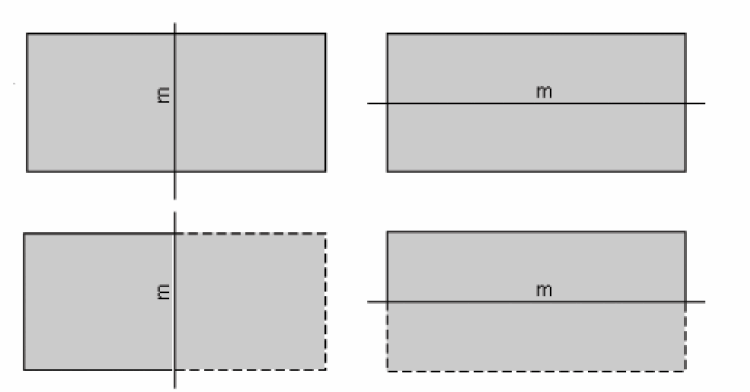
Les rectangles montrés ci-dessus possèdent deux plans de symétrie. Des objets plus complexes et en trois dimensions peuvent avoir un nombre plus élevé. Par exemple, un hexagone ne possède pas seulement un axe de rotation d’ordre 6, mais également 6 plans de symétrie.

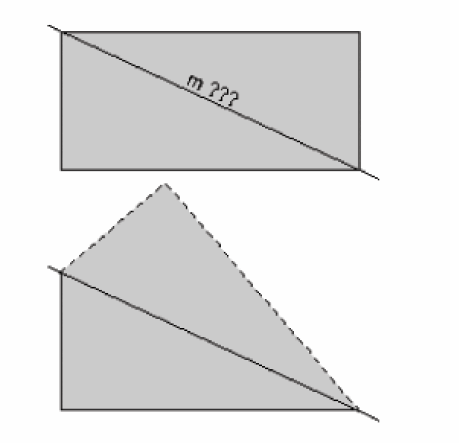
Notons qu’un rectangle ne possède pas de plan de symétrie le long de sa diagonale. Si nous coupons le rectangle le long de sa diagonale notée m ??? sur le diagramme supérieur de la figure ci-contre, la partie réfléchie par un miroir est celle qui est représentée par des pointillés dans le diagramme inférieur. Comme l’image inférieur ne reproduit pas le rectangle initial, la ligne m ??? n’est pas un plan de symétrie.

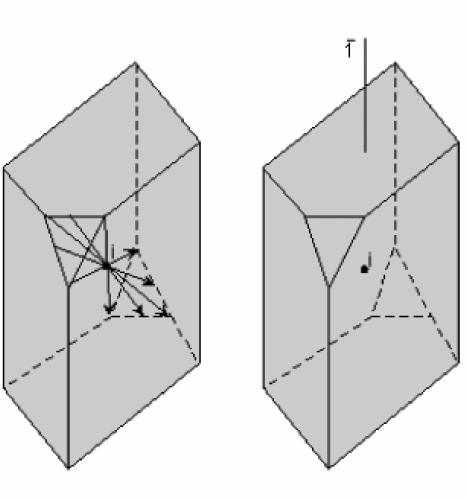
C’est un point imaginaire situé au centre géométrique du cristal de façon telle que les sommets, faces et arêtes de ce cristal se correspondent deux à deux sur une ligne passant par ce centre et qu’ils en soient à égale distance.

Dans l’exemple ci-contre, au triangle situé sur l’une des arêtes du cristal correspond le même triangle inversé de l’autre coté du cristal. Le centre de symétrie i est tel qu’à tout point M du triangle correspond un point M’ situé sur la droite joignant M à ce centre et à la même distance. Seules quelques droites ont été figurées sur le diagramme de gauche. A droite, le diagramme montre le cristal sans les droites imaginaires qui reproduisent le triangle.

Le centre de symétrie est symbolisé par la lettre i ou C. Au contraire des autres éléments de symétrie, il ne peut exister qu'un seul centre d'inversion dans un objet.

Si le cristal possède un axe de symétrie et un centre de symétrie, alors l’axe (ou les axes) de symétrie passeront par ce centre de symétrie.

On dit qu’une figure possède un axe de symétrie inverse si elle est superposable à elle- même par la transformation résultant d’un déplacement (rotation autour d’un axe de symétrie directe) suivi d’une symétrie par rapport à un point situé sur l’axe (inversion). Les principaux axes de symétrie inverse sont les suivants :

a. Axe de symétrie inverse d’ordre 2

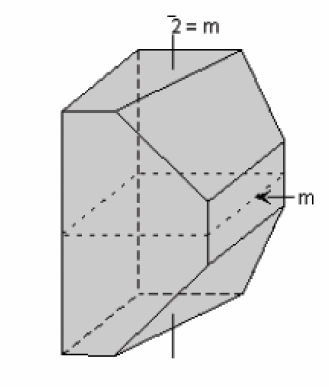
Une figure possède un axe de symétrie inverse d’ordre 2 si elle est superposable à elle-même par la transformation résultant d’une rotation de 180° suivi d’une inversion. Cette opération est équivalente à avoir un plan de symétrie m perpendiculaire à cet axe de symétrie. Cet axe est symbolisé par : 2 ou A 2.

b. Axe de symétrie inverse d’ordre 3

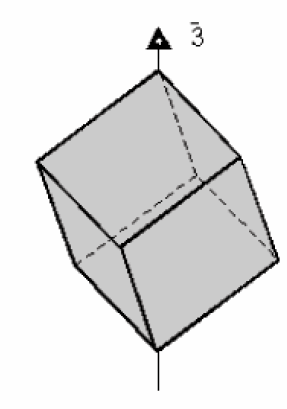
Une figure possède un axe de symétrie inverse d’ordre 3 si elle est superposable à elle-même par la transformation résultant d’une rotation de 120° (360/120 =3) suivi d’une inversion. Le cube est un bon exemple d’un objet possédant un axe de symétrie inverse d’ordre 3. Cet axe est symbolisé par : 3 ou A 3.

Notons que cette opération est identique à celle d’avoir un axe de symétrie d’ordre 3 et un centre de symétrie.

c. Axe de symétrie inverse d’ordre 4

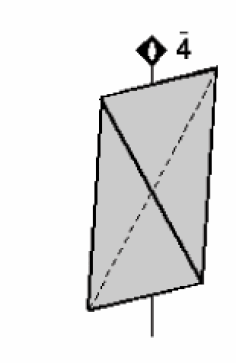
Une figure possède un axe de symétrie inverse d’ordre 4 si elle est superposable à elle-même par la transformation résultant d’une rotation de 90° suivi d’une inversion. Cet axe est symbolisé par : 4 ou A 4.

d. Axe de symétrie inverse d’ordre 6

Une figure possède un axe de symétrie inverse d’ordre 6 si elle est superposable à elle-même par la transformation résultant d’une rotation de 60° suivi d’une inversion. Cet axe est symbolisé par : 6 ou A 6.

Notons que cette opération est identique à celle d’avoir un axe de symétrie d’ordre 3 perpendiculaire à un plan de symétrie.

Remarque : L’axe de rotation inverse d’ordre 1, résultant d’une rotation de 360° suivi d’une inversion, est équivalent à un centre de symétrie.

Il est évident que les objets à trois dimensions, comme les cristaux, peuvent posséder plusieurs éléments de symétrie. Et comme il y’a des relations obligatoires entre les divers éléments de symétrie, il s’ensuit qu’un cristal ne pourra posséder en même temps qu’un certain nombre d’entre eux. En fait, dans les cristaux, il existe 32 combinaisons possibles entre les éléments de symétrie. Ces 32 combinaisons définissent les 32 classes cristallines. Chaque cristal doit appartenir à l’une de ces 32 classes cristallines. Dans le prochain cours, nous décrirons chaque classe en détail.

Nous allons voir dans ce paragraphe un exemple de cristal ou plusieurs éléments de symétrie peuvent se combiner. Nous insisterons sur un point important : les éléments de symétrie d’une même figure ne sont pas tous indépendants et la présence simultanée de plusieurs de ces éléments entraîne souvent l’existence nécessaire d’autres éléments. Ceci doit être clair comme nous le verrons dans l’exemple suivant.

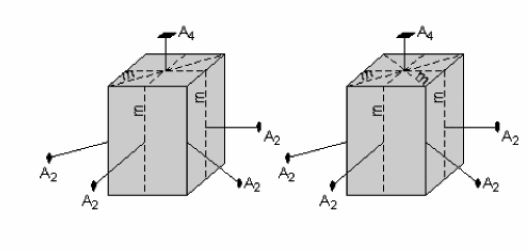
Dans cet exemple, on considère un cristal possédant des côtés rectangulaires limités en haut et en bas par deux carrés. Le carré du haut indique que le cristal possède un axe de symétrie d’ordre 4, perpendiculaire au centre du carré comme cela est représenté sur la figure.

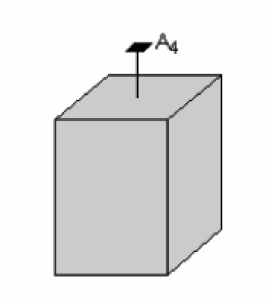
Notons aussi que la face rectangulaire du côté droit du cristal possède un axe de symétrie d’ordre 2. Cet axe de symétrie traverse le cristal et ressort du côté gauche (non visible sur la figure) ; ainsi les deux côtés droit et gauche du cristal sont perpendiculaires à l’axe de symétrie d’ordre 2.

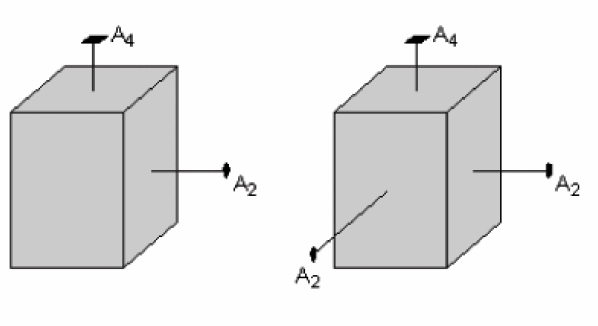
Comme la face supérieure du cristal possède un axe de symétrie d’ordre 4, l’opération de rotation d’ordre 4 reproduit les faces rectangulaires du cristal avec leur axe de symétrie d’ordre 2 après une rotation de 90°. Donc, les deux faces avant et arrière du cristal possèdent aussi un axe de rotation d’ordre 2 qui leur est perpendiculaire, et notons que cela a été déduit à partir de l’existence de l’axe d’ordre 4.

La face carrée du haut indique que le cristal possède un axe de rotation d’ordre 2 qui recoupe diagonalement le cristal. Cet axe est visible sur le diagramme de gauche (figure ci-contre). Mais l’existence de l’axe de symétrie d’ordre 4 implique que l’autre diagonal doit posséder un axe de symétrie d’ordre 2, comme cela est figuré sur le diagramme de droite.

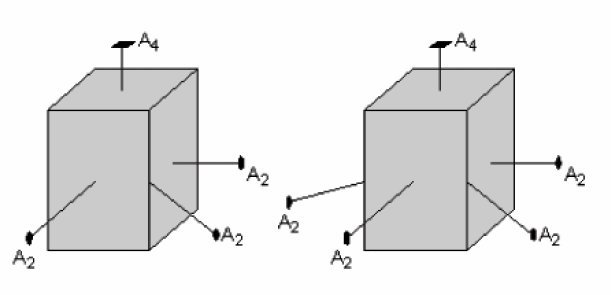
En outre, le carré du haut et la face rectangulaire du devant indiquent l’existence d’un plan de symétrie comme cela est visible sur le diagramme de gauche de la figure ci-contre.

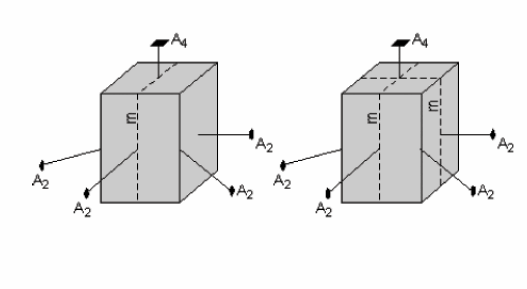
Mais encore ici, l’opération de rotation d’ordre 4 exige l’existence d’un deuxième plan de symétrie comme cela est visible sur le diagramme de droite.

Le carré de la face supérieure du cristal indique aussi l’existence d’un plan de symétrie qui recoupe diagonalement le cristal. Ce plan de symétrie peut être réfléchie par les deux autres

miroirs, ou reproduits par l’axe de symétrie d’ordre 4, et ainsi le cristal doit posséder un autre plan de symétrie qui recoupe l’autre diagonal du cristal, comme cela est visible sur le diagramme de droite de la figure précédente.

Finalement, il existe un autre plan de symétrie qui recoupe horizontalement le cristal.

Finalement, le cristal possède les éléments de symétrie suivants :

• 1 axe de symétrie d’ordre 4 (A4)
• 4 axes de symétrie d’ordre 2 (A2), 2 qui recoupent les faces du cristal et 2 qui recoupent les bords.
• 5 plans de symétrie (m), 2 recoupant verticalement les faces, 2 recoupant les bords et
• 1 recoupant horizontalement le centre du cristal.
• Un centre de symétrie i.

Les éléments de symétrie de ce cristal sont : i, 1A4, 4A2, 5m.

Cours présenté par : CHABOU Moulley Charaf