Qu’est-ce que l’Astronomie ?
L'Astronomie est une science
Les sciences proposent une démarche particulière pour énoncer des lois. Cette démarche consiste à définir un protocole d'expérience (les règles du jeu), à réaliser des expériences suivant ce protocole, puis à en analyser les résultats (les réponses de la Nature).
Donnons un exemple : attachons une bille de plomb à un fil, et attachons le fil à un crochet. On peut faire balancer la bille au bout de son fil (en l'écartant peu de la verticale). Elle met un certain temps pour faire un aller-retour. Si nous allongeons le fil, ce temps s'allonge. Nous définissons un protocole d'expérience en décidant : - de faire plusieurs mesures, avec des longueurs de fil de 0,50 mètre, 1 mètre, 1,5 mètre... - Et pour chaque longueur, on notera le temps mis par la bille pour faire un aller-retour. Pour que le résultat soit plus précis, on détermine le temps mis pour faire 10 balancements, et on le divise par 10. On réalise ces expériences, et on note les temps mesurés dans un tableau.
Après cette analyse, on tente de formuler des lois. Dans l'exemple donné, on remarquera qu'on obtient toujours le même nombre (à peu près 4,025) si on divise le carré du temps par la longueur du fil. On va considérer cette relation comme une loi potentielle, qu'il convient de valider. On refait des expériences, en variant la longueur du fil, et chacune doit vérifier la loi.
L'essentiel est que ces expériences doivent être reproductibles, par d'autres personnes, en d'autres lieux. Si les lois obtenues sont contredites par une seule autre expérience, elles sont abandonnées. Cette méthode permet d'avancer vers une connaissance de plus en plus fine et de plus en plus correcte de la nature. Dans notre exemple, il convient de refaire les mesures avec des fils de toutes longueurs, et en tout lieu : on confirmera la relation, si on s'en tient à des mesures simples, disons au dixième de seconde près. Si on augmente la précision des mesures, on s'apercevra que la loi reste vraie dans son principe, mais que la valeur obtenue peut varier d'un lieu à l'autre : ce n'est pas partout exactement 4,025. Il conviendrait donc de raffiner la loi, de la préciser pour qu'elle tienne compte d'un facteur secondaire qu'on avait ignoré jusque là, et incorporé dans cette faussse constante. Les scientifiques ont le courage d'énoncer et de publier des lois précises, vérifiables (ou réfutables...) par tout le monde. D'ailleurs, pour être un grand scientifique, il est bon de réfuter une théorie antérieure, et de proposer la sienne, qui va plus loin dans son adéquation avec la Nature.
Nous verrons plus loin l'explication du mouvement des planètes, mais historiquement, les choses se sont passées ainsi :
- d'abord, constatation que les planètes tournent autour du soleil, sans savoir pourquoi (Copernic) ;
- puis, établissement des lois de Kepler, formules mathématiques permettant de faire des calculs, pour représenter les mouvements, sans savoir pourquoi ;
- ensuite, une première explication formulée par Newton, avec la notion de force, mystérieuse action à distance instantanée ;
- enfin, la théorie géométrique d'Einstein, qui raffine la théorie de Newton, tient compte d'effets secondaires, la précise et lui donne une base plus claire.
L'Histoire en est là, peut-être n'est-elle pas finie...
Notre propos sera donc d'expliquer tout cela, avec les méthodes scientifiques disponibles aujourd'hui. Nous proposerons quelques expériences simples pour aider la compréhension.
Science et croyance
Pour en finir avec la méthode scientifique, rappelons qu'il ne faut pas confondre Astronomie et astrologie. L'astrologie n'est pas une science, même si elle s'affuble parfois de ses oripeaux. Elle ne fait aucune expérience, elle ne se base que sur une connaissance encyclopédique, empirique, venue de la nuit des temps, sans en maîtriser l'origine. Rien n'est reproductible. Mars est associée au sang, à la guerre, à cause de sa couleur rouge... due à des oxydes de fer ! L'analogie de couleur a donné toute une interprétation, qui n'a plus aucun sens depuis qu'une sonde a analysé le sol de la planète. L'astrologie est basée essentiellement sur l'ignorance.
Les énoncés des astrologues sont toujours vagues. Ils font intervenir des paramètres divers, selon les circonstances. Leurs prédictions sont assez floues pour masquer leurs erreurs. Une expérience a été faite dans une université américaine : une lettre personnalisée a été adressée à une centaine d'étudiants, en leur demandant si le portrait qu'elle dressait leur était ressemblant. 90 % d'entre eux ont répondu oui... alors que le portrait était le même pour tous !
Plus grave, l'astrologie ignore les réalités astronomiques sur lesquelles elle prétend se baser, et nous verrons plus loin que même les signes du zodiaque ne correspondent plus maintenant à leur constellation ! Le succès de l'astrologie est dû au flou qui entoure toujours ses prédictions, permettant d'interpréter a posteriori de la manière la plus favorable. C'est le contraire de la Science, dont les règles rigoureuses sont sans ambiguité : elles expliquent correctement les phénomènes de la Nature, ou pas.
La notion de science que nous avons maintenant s'est forgée lentement au cours des siècles. Tout ce qui touche au ciel (auquel on n'a pas accès) a toujours eu une connotation magique, religieuse. Kepler, l'un des premiers qui ait appliqué des méthodes scientifiques, qui nous a donné les lois régissant le mouvement des planètes, n'a pas échappé à cette tendance, et il a gagné sa vie en... rédigeant des horoscopes ! Mais à côté de cette activité lucrative, il a fait une immense œuvre scientifique : avant lui, la seule explication possible du ciel était religieuse, tirée de la Bible qu'il fallait lire littéralement (création du ciel et de la Terre, de la Lune et des étoiles, puis de l'Homme, en 7 jours ; âge de la Terre déduit des générations de personnages bibliques...).
Claude Ptolémée, dans l'Antiquité, a défini un système du monde, constitué de cercles (seule courbe parfaite) parcourus par les planètes d'un mouvement uniforme (mouvement parfait). Comme les vrais mouvements ne sont pas uniformes, il a dû compliquer son système en plaçant le centre d'un cercle sur un autre cercle... Pour lui, Soleil, Lune, planètes, étoiles, tournaient autour de la Terre ! En accord avec les apparences immédiates... Cette analyse ne permettait pas de prédire correctement les positions des planètes. Le système géocentrique (la Terre au centre) de Ptolémée, qui n'explique rien, mais se contente de décrire les apparences, était acceptable pour les religieux, et a été le seul enseigné pendant tout le Moyen Age. Dommage, car Aristarque de Samos avait déjà compris que la Terre tourne autour du Soleil en 280 avant JC...
Kepler a montré qu'une étude raisonnée pouvait être plus fructueuse, puisqu'elle lui a permis de découvrir les lois du mouvement. Mais il a dû faire preuve pour cela d'une grande indépendance d'esprit. On sait ce qu'il pouvait en coûter, en pensant au procès de Galilée, et à la fin tragique de Giordano Bruno.
Maintenant, admettons que la Science n'est pas la Vérité !
La Science est la recherche de la vérité. Ce n'est pas du tout la même chose... Ce que nous croyons aujourd'hui en matière scientifique n'attend qu'une réfutation future... Mais la réfutation d'une loi porte en germe l'ouverture vers d'autres lois, voire vers d'autres branches de la science. C'est ce qui est arrivé au début du XXéme siècle. A la fin du siècle précédent, la Physique était achevée ! Tout était connu et compris..., sauf trois petits détails insignifiants :
- l'avance du périhélie de Mercure,
- le rayonnement du corps noir,
- et l'effet photoélectrique.
Un astrologue aurait invoqué des influences mauvaises, les scientifiques en ont tiré la Mécanique Quantique, la Relativité Restreinte et la Relativité Générale. Une vision complètement nouvelle du Monde, un bouleversement si riche qu'il permet en particulier d'envisager une compréhension globale de l'Univers ! Des applications qui permettent de fabriquer des lasers (optique quantique), des téléviseurs (relativité restreinte dans les écrans vidéo), des GPS (relativité générale)... Sans ces trois petits détails et leurs conséquences, notre vie quotidienne ne serait pas ce qu'elle est. Mais pour en arriver là, il a fallu se remettre totalement en question. Ce qui est le propre des scientifiques, ou plus précisément de la méthode, du système scientifique.
Les scientifiques ne sont pas parfaits, ils commettent sans cesse des erreurs, mais la méthode scientifique porte en elle les moyens de corriger ses erreurs.
Laissons donc les aspects religieux ou ésotériques pour essayer de comprendre la réalité de l'Univers qui nous entoure. Tout le monde a entendu parler de planètes, de satellites, de nébuleuses, de galaxies, de quasars, de trous noirs... Ces mots sont apportés par certains journalistes qui font œuvre louable en parlant de science de temps en temps, mais attention aux erreurs parfois (souvent ? ! ) commises. Le but de ces notes sera d'expliquer progressivement toutes ces notions mais... commençons par ce qui nous entoure !
Regarder le ciel
L'instrument d'observation : l'œil
L'œil est le premier instrument d'observation, et le seul pour la plupart des gens ! Et le seul pendant des millénaires... Il faut apprendre à s'en servir.
Tout d'abord, savoir qu'il n'est pas parfait, même quand on est tout jeune...
Pensez à une voiture qui vient vers vous la nuit, dans une vaste plaine (pas forcément morne...) : de très loin, vous voyez la tache de ses phares... LA tache ? Elle a pourtant DEUX phares ! Mais maintenant qu'elle s'approche en effet, vous en voyez deux. Vous ne vous êtes jamais posé de question à ce sujet ? C'est tellement naturel, qu'on n'y prête aucune attention, et pourtant, il y a une explication.
Constitution de l'œil
L'œil comprend une lentille convergente, le cristallin, et une surface sensible, la rétine, sur laquelle se forment les images (il a la même structure qu'un appareil photo, à moins que ce soit l'inverse).
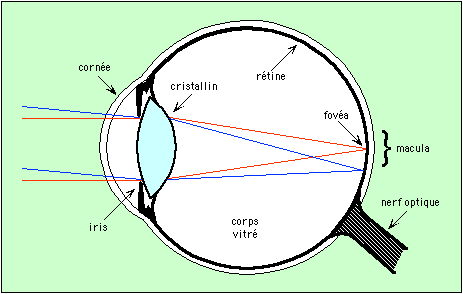
La rétine est constituée de minuscules cellules juxtaposées, sensibles à la lumière. Chacune indique au cerveau si elle reçoit de la lumière. Le schéma montre que les images de deux étoiles, une bleue et une rouge, vont se former sur la rétine.
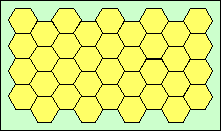
Schéma de la rétine, montrant les cellules sensibles juxtaposées.
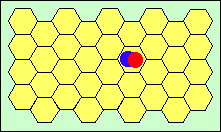
Deux images se forment sur la même cellule ; on ne voit qu'un seul point.
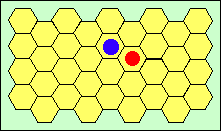
Les deux images sont plus éloignées, et excitent deux cellules différentes. Elles sont bien visibles séparément.
L'œil peut donc distinguer séparément deux objets à condition que leurs images se forment sur deux cellules différentes. Sinon, la seule cellule touchée indiquera au cerveau qu'il voit un seul objet. La taille des cellules de la rétine fait que l'œil peut distinguer deux objets à condition qu'ils soient séparés par un angle d'au moins 1' (lire : une minute). Lorsque la voiture est trop loin (disons au moins 5 km), l'angle sous lequel on voit ses phares est plus petit que 1', et donc les images des deux phares tombent sur la même cellule de la rétine ; nous ne voyons qu'une seule tache lumineuse.
Reprenons la voiture au loin, mais observons-la maintenant avec des jumelles. Nous allons bien distinguer les deux phares. On dit qu'un instrument d'optique a un pouvoir séparateur. Cette locution imagée (naturellement ! ) indique qu'il est capable de vous montrer deux objets, et non un seul, là où il y en a effectivement deux. Les jumelles ont un pouvoir séparateur meilleur que l'œil. Un grand télescope a un pouvoir séparateur encore meilleur que des jumelles. En d'autres termes, cela signifie qu'il nous permettra de voir de plus petits détails. Dans le ciel, il y a de nombreuses étoiles doubles, et il faut parfois de puissants instruments pour les distinguer.
Ceci étant, le pouvoir séparateur de l'œil est d'une minute d'arc (notée 1')... La belle affaire !
- le cercle est divisé en 360°, (lire : 360 degrés d'arc, ou simplement 360 degrés) ; chaque degré est divisé en 60' (lire : 60 minutes d'arc, ou simplement 60 minutes) et chaque minute est encore divisée en 60" (lire : 60 secondes d'arc, ou simplement 60 secondes). Il y a donc 360 × 60 = 21.600' dans le cercle, ou bien 360 × 60 × 60 = 1.296.000". Mais ceci n'est pas très parlant ;Pour comprendre, voici un cercle avec trois rayons. L'angle entre les rayons rouge et vert vaut 60°, et celui entre les rayons vert et bleu vaut 10°. Cette dernière valeur représente donc, à nos yeux, un petit angle.
- la pleine lune a un diamètre apparent de 30' ; donc à l'œil nu, on peut y voir des détails trente fois plus petits qu'elle-même ;
- 1' correspond à l'angle sous lequel on voit une pièce de 1 euro (23 mm) à 79 mètres....
- l'angle formé par les deux lignes ci-dessous fait à peu près 20' :

Expérience : Réalisez le schéma ci-dessous sur du papier fort, et percez les deux trous représentés sur le dessin. Ils doivent être séparés de 3 mm (entre les centres des trous).

Placez une ampoule derrière, et observez à 10 mètres... Vous aurez la même sensation qu'en regardant deux étoiles séparées d'une minute d'arc.
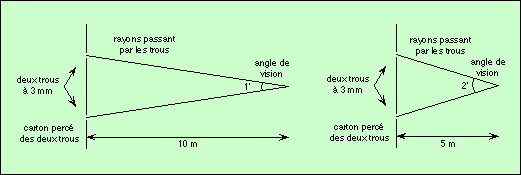
Si vous ne distinguez qu'un seul trou, c'est que vous êtes au-dessous du pouvoir séparateur de votre œil. En vous rapprochant (partie droite du schéma ci-dessus), vous augmenterez l'angle entre les trous et vous arriverez à les distinguer.
Voici l'angle sous lequel on voit les deux trous, selon la distance à laquelle on se trouve :
| distance | 20 m | 15 m | 10 m | 7 m | 5 m | 3 m | 2 m | 1 m |
| angle | 30″ | 40″ | 1′ | 1′ 30″ | 2′ | 3′ 30″ | 5′ 10″ | 10′ 20″ |
Le pouvoir séparateur de l'œil normal est d'une minute d'arc, mais de multiples défauts peuvent l'altérer.
Le but d'un instrument astronomique est d'augmenter l'angle sous lequel on voit un objet, pour le faire passer au-dessus du pouvoir séparateur de l'œil. Ce qui nous donne l'impression de nous en rapprocher !
Vision nocturne
La rétine est constituée de deux sortes de cellules sensibles différentes, les cônes et les bâtonnets. Les premières détectent la couleur, mais sont relativement peu sensibles, elles servent en vision diurne. Les autres ne voient pas la couleur, mais sont très sensibles à la moindre lumière. Elles sont disposées différemment dans la rétine :
- La plus grande partie de la rétine ne contient que des bâtonnets ;
- Le fond, où se forme l'image d'un objet qu'on regarde en face, contient essentiellement des cônes. On le nomme macula (tache) ;
- Le centre de la macula (fovéa) ne contient que des cônes, aveugles la nuit, mais donne la finesse maximum en pleine lumière.
Ainsi, dans des conditions de faible éclairement, ce seront les bâtonnets qui nous permettront de voir, mais en noir et blanc... Ce n'est pas pour rien que la nuit, tous les chats sont gris !
Ces rapides explications vous permettront de comprendre un phénomène bien connu des astronomes : lorsque vous regardez un objet vraiment faible, il ne faut pas chercher à le regarder bien en face, en centrant son image sur la fovea, au centre de la rétine. Il vaut mieux regarder un peu à côté, comme pour l'ignorer... Ce seront alors les bâtonnets sensibles qui agiront, et vous aurez la surprise de bien le distinguer... sans couleurs évidement.
La rétine contient 130 millions de bâtonnets, mais seulement (!) 6.500.000 cônes ! Résumons :
bâtonnets :faible performancegrande sensibilitépartoutnoir et blancvision nocturnevision scotopiquecônes :hautes performancesfaible sensibilitéau centre de la rétinecouleurvision diurnevision photopique
Scotopique est synonyme de nocturne, et photopique est synonyme de diurne. Ce sont les termes savants... pour mémoire.
Lieu d'observation
La Déclaration Universelle des Droits des Astronomes n'est pas encore signée !
Certains prétendent qu'il y a une difficulté majeure pour la signature. Laquelle ? Nous allons faire une petite expérience :
Placez-vous au centre d'une pièce. Penchez la tête en arrière pour voir le plafond juste au-dessus de vous. Maintenant, tournez sur vous-même : vous voyez toujours la même chose (le plafond et le haut des murs), seule l'orientation change.
Mettez maintenant la tête à l'horizontale : vous voyez une partie du plafond, le mur qui vous fait face, et une partie du plancher. Tournez ; vous voyez à mesure les autres parties du plafond, les autres murs, et les autres parties du plancher !
Donc, si votre regard se porte perpendiculairement à l'axe de rotation (deuxième cas), vous découvrirez en tournant la totalité de ce qui vous entoure. Les astronomes se trouvant à différents endroits de la Terre sont confrontés à ce phénomène :
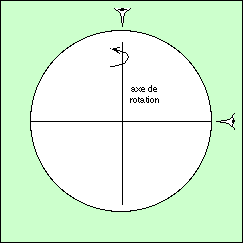
Au pôle (Nord), le regard dirigé vers le ciel est dans l'axe de rotation, on voit la moitié (Nord) de la sphère céleste, qui tourne par rapport au sol. L'autre moitié (Sud) est inaccessible au-dessous de l'horizon ! Ca tombe bien, il y fait trop froid...
A l'équateur, le regard tourné vers le ciel est perpendiculaire à l'axe de rotation. Bien sûr, chaque nuit on ne voit qu'une moitié du ciel, mais le déplacement de la Terre autour du Soleil nous présente successivement, au cours de l'année, toutes les parties de la sphère céleste.
Du temps où les moyens de transport étaient lents et hasardeux, on construisait les observatoires là où on était, et s'accomodait des conditions locales. Avec les progrès techniques, il est devenu intéressant de les construire près de l'équateur.
A l'équateur même, les étoiles proches des pôles ne seraient jamais observables correctement, car elles seraient toujours à l'horizon, noyées dans les brumes. Les grands observatoires ont donc été construits aux latitudes moyennes, dans les deux hémisphères.
Aujourd'hui, les choses changent encore. En Antarctique, on dispose d'une nuit de cinq mois, pendant laquelle des observations pourront se poursuivre très longtemps, sans interruption par le Soleil. Et pendant l'été austral, c'est le Soleil lui-même qui peut être observé 24 heures sur 24. Bien que les conditions climatiques y soient sévères, des projets sont en cours de réalisation.
Pollution lumineuse
La proximité des grandes villes interdit l'observation astronomique, par la quantité de lumière que les divers éclairages jettent dans le ciel. Depuis l'espace, de nombreuses photographies de la Terre ont été faites de nuit ; il est impressionnant de voir les taches lumineuses associées aux grandes villes et aux agglomérations. La région de Londres est particulièrement brillante. Seuls certains déserts, comme le Sahara, sont pour le moment épargnés. Il est bien évident que les grands télescopes, qui chassent la moindre goutte de lumière tombant des étoiles, ne peuvent supporter un tel voisinage.
Turbulence atmosphérique
Il reste encore une difficulté, et non des moindres. Elle est induite par l'atmosphère. C'est la turbulence qui affecte les images. On peut s'en faire une idée en observant une route surchauffée en été. On voit l'air chaud qui tremble au-dessus, et qui déforme les objets situés plus loin. Ce phénomène se produit également dans les couches de l'atmosphère au-dessus de nos têtes, et fait trembler les images. C'est lui qui produit le scintillement des étoiles. Il limite le pouvoir séparateur d'un instrument à 0,5 " au mieux. Cette limite est le seeing.
Pour diminuer l'importance de la turbulence, la solution la plus simple consiste à diminuer l'épaisseur de l'atmosphère, ce qui se réalise très facilement en installant les télescopes à haute altitude.
Un autre avantage de l'altitude se trouve dans la grande sécheresse de l'air. La vapeur d'eau présente dans les basses couches de l'atmosphère gêne les observations en filtrant certaines radiations, et par son dépôt sur les instruments sous forme de rosée. Enfin, en se condensant, elle produit les nuages. A haute altitude, on se trouve souvent au-dessus des nuages.
Lieux favorables
Pour trouver un site favorable à l'observation, il faut découvrir un endroit où :
- le temps est toujours beau (absence de nuages),
- la vapeur d'eau est presque absente de l'atmosphère (observations en IR),
- l'atmosphère est la plus légère possible (il n'en reste plus que la moitié au-dessus de 4.000 m),
- le ciel est accessible dans sa plus grande partie (proche de l'équateur),
- la présence humaine (lumières) est quasiment nulle,
- la turbulence est minimale.
Le beau temps (1) et l'absence de vapeur d'eau (2) indiquent les déserts (qui satisfont 5). D'ailleurs, les déserts se trouvent dans la zone équatoriale (4 en plus). Plus on s'élève en altitude, plus la couche d'atmosphère au-dessus de la tête diminue (3). Enfin, la proximité de la mer assure une stabilité des températures, et par conséquent des différences faibles entre jour et nuit. Ceci est favorable pour diminuer la turbulence (6). Au bout du compte, les déserts proches de la mer et à haute altitude sont les régions les plus indiquées pour installer les observatoires modernes.
En résumé, les meilleurs sites se trouveront donc en altitude, proches de la mer (ou en plein milieu, sur une île...), loin des villes et dans une zone au climat désertique.
Il y a des lieux sur Terre qui conjuguent ces trois conditions :
- les grands volcans, dans les îles Hawaii (Mauna Kea, 4.200 m...) ;
- les Canaries (Roque de los Muchachos, 2.600 m) ;
- le désert d'Atacama, dans la Cordillère des Andes, au Chili (La Silla 2.400 m, Cerro Tololo 2.400 m, Cerro Paranal 2.635 m...).
Dans ces zones, l'air est très sec, la turbulence atmosphérique très faible, et les nuages rares. Aucune grande ville ne se trouve à proximité. Presque tous les grands télescopes modernes sont installés en ces lieux. Au Cerro Paranal, on atteint les 360 nuits de beau temps par an !!
Les sites d'Amérique du sud sont toutefois sujets à des séismes fréquents, car situés sur une palque tectonique (Nazca) en mouvement. Les coupoles du VLT ont été construites aux normes antisismiques...
Pour être complet, il faut toutefois signaler un nouveau lieu d'excellente qualité : c'est l'Antarctique ! La nuit y dure 6 mois, autorisant des observations de très longue durée... Le froid glacial qui y règne pendant la nuit (c'est-à-dire pendant l'hiver), supprime toute vapeur d'eau dans l'atmosphère. L'altitude y est élevée : 3.000 mètres au Dôme C. Toutes ces conditions sont parfaites pour l'astronomie, à la condition de protéger le matériel... et les astronomes, du froid. Une étude précise faite par Eric Fossa (Observatoire de Nice) indique qu'au niveau du sol (pardon, de la glace), la turbulence est très élevée, rendant toute observation illusoire (vents catabatiques). Mais à une vingtaine de mètres au-dessus du sol, l'air est d'une stabilité impressionante, meilleur que dans tous les autres sites mondiaux. Malgré les difficultés très grande d'installation d'un observatoire sur pilotis dans un tel lieu, Eric Fossa pense bien parvenir à réaliser son rêve d'observatoire vraiment austral !
Maintenant, nous savons l'essentiel sur la constitution de notre œil, et nous savons où mettre nos télescopes. Il est temps de s'intéresser aux messages que les astres nous envoient, tout d'abord la lumière visible.
La lumière
La lumière est restée le seul moyen de connaissance de l'Univers, jusqu'au XXème siècle. Ses propriétés ont été exploitées à fond par les astronomes pour en tirer la position, la couleur, la température, la composition chimique, le magnétisme, la vitesse... des étoiles et des objets plus curieux qu'ils ont découverts par la suite.
Plus généralement, la lumière n'est qu'un rayonnement électromagnétique parmi tant d'autres, et nos moyens modernes d'observation nous permettent de les utiliser tous. Chaque gamme donne des renseignements particuliers, et l'ensemble nous permet d'atteindre une grande richesse d'information sur les objets qui nous entourent. Les rayons électromagnétiques sont assez complexes pour porter un grand nombre d'informations, de natures diverses.
Depuis les années 1920, la théorie de la Relativité d'Einstein permet de comprendre l'état actuel et l'évolution de l'Univers dans son ensemble. Cette théorie est basée sur la vitesse de la lumière, qui est très proche de 300.000 kilomètres par seconde.
A cette vitesse, la lumière met 1,3 secondes pour aller de la Terre à la Lune, 8 minutes pour aller du Soleil à la Terre, 6 heures pour aller du Soleil à Pluton...
Mais elle met 4,2 années pour nous parvenir de l'étoile la plus proche. Ceci a une conséquence très importante : nous voyons l'étoile la plus proche non telle qu'elle est actuellement, mais telle qu'elle était il y a 4,2 années !
Et plus on voit loin, plus les objets qu'on observe sont vieux. Les objets les plus lointains qu'on puisse voir actuellement sont situés à près d'une dizaine de milliards d'années lumière, autant dire qu'on les voit maintenant tels qu'ils étaient il y a une dizaine de milliards d'années. Beaucoup de ces objets ont sans doute disparu, en tout cas ils ont considérablement évolué depuis, mais nous ne pouvons pas le savoir.
Toutefois, en observant des objets à des distances différentes, donc à des âges différents, on peut arriver à reconstituer leur évolution. Supposez que vous ignoriez tout des arbres, et qu'on vous emmène dans une forêt. Il vous serait assez facile de reconnaître des sapins (par exemple), même s'ils sont tous d'âges différents. Vous auriez vite compris comment ils poussent.

Le système de l'Univers, dessin du Moyen-Age
A l'heure actuelle, nous disposons d'instruments capables de capter tous les rayonnements électromagnétiques (presque...), depuis les ondes radio jusqu'aux rayons gamma. Il se trouve que les astres émettent toutes ces sortes d'ondes, chacun ayant une gamme de fréquences déterminée par sa nature physique, et par l'énergie disponible. Beaucoup de ces rayonnements ne parviennent pas au sol, car ils sont arrêtés par l'atmosphère. Il faut donc construire des observatoires orbitaux capables de travailler dans ces domaines d'ondes. Toute une nouvelle branche de l'astronomie s'est constituée depuis l'avènement des fusées et des satellites.
Terre, Lune et Soleil
Quand on regarde le ciel, on peut y voir deux objets montrant une surface sensible : la Lune et le Soleil (il en existe trois autres, la galaxie d'Andromède dans l'hémisphère nord, et les deux galaxies satellites de la nôtre, le Grand et le Petit Nuage de Magellan, dans l'hémisphère sud).
Tout le reste se présente comme de simples points lumineux plus ou moins brillants.
Ces points lumineux conservent toujours les mêmes positions relatives. Ils forment sur le ciel des dessins plus ou moins évidents, qu'on a nommés constellations. L'ensemble constitue la sphère des fixes des Anciens.
Mais 5 points lumineux se particularisent : ils se déplacent par rapport à la sphère des fixes. Pour cela, les Grecs les ont nommés planètes, mot qui signifie astre errant. Remarquez que d'après cette éthymologie, le Soleil et la Lune sont aussi des planètes ; mais cette appellation, basée sur le seul mouvement et faisant fi des profondes différences physiques, n'est plus de mise en astronomie.
Dans cette belle ordonnance du ciel, il arrive parfois qu'un intrus apparaisse : les comètes ne pouvaient donc qu'être maléfiques, annonciatrices de guerres ou de calamités (mais des guerres, il y en a malheureusement toujours une pour associer à une comète, et si jamais il n'y en avait pas, une simple sécheresse, une gelée tardive au printemps... permettait de justifier ce caractère maléfique des comètes).
Il reste enfin un phénomène rare, celui des novæ (pluriel de nova = nouvelle). Ce sont des étoiles qui explosent, et deviennent subitement beaucoup plus lumineuses, permettant de les voir à l'œil nu. Les chinois les appelaient joliment étoiles invitées.
Voilà donc le ciel des Anciens (il y a sans doute encore beaucoup d'Anciens à l'heure actuelle, qui n'ont jamais cherché à en savoir davantage... et qui en restent aux apparences).
Jusqu'au Moyen Age, la Terre était souvent vue plate, et n'avait rien de commun avec la Lune ou le Soleil. Mais maintenant nous savons bien que c'est une sphère (certains grands esprits de l'Antiquité le savaient déjà, voir la fiche historique).
La Terre est une planète. Une planète est un corps qui ne produit pas de lumière, par opposition aux étoiles. La Terre tourne autour du Soleil, qui est une étoile.
La Lune est un satellite de la Terre (elle tourne autour de la Terre). Un satellite (naturel) est un corps semblable à une planète, mais qui tourne autour d'une planète.
La Lune nous paraît grosse car elle est relativement proche. Pour l'instant, nous ne nous occuperons que de la Terre et du Soleil.
Les lois du mouvement
Expérience
Lançons une bille d'acier sur une table horizontale bien lisse, elle continue en ligne droite. Si nous voulons qu'elle aille plus vite, il faut la pousser encore. Si nous voulons qu'elle aille moins vite, il faut la freiner. Donc, pourquoi s'arrêterait-elle ? Simplement parce qu'il y a une force invisible, occasionnée par les frottements sur la table et la résistance de l'air. On peut diminuer les frottements en remplacant la table par un marbre très bien poli. Si on pouvait supprimer totalement les frottements, la bille continuerait indéfiniment en ligne droite. C'est le principe d'inertie :
Un corps, non soumis à des forces extérieures,continue indéfiniment son mouvement uniforme en ligne droite
Plaçons un aimant sur la table. Plaçons ensuite la bille d'acier à quelque distance, et lâchons-la sans la lancer. La bille se met en mouvement en direction de l'aimant, elle va de plus en plus vite et fini par se coller à l'aimant. L'aimant exerce donc une attraction sur la bille.
Laissant l'aimant sur la table, lançons la bille. Pour respecter le principe d'inertie, elle devrait aller tout droit. Pour répondre à l'attraction de l'aimant, elle devrait aller vers lui. Elle va concilier les deux en suivant une trajectoire courbée.
Les planètes sont soumises à des lois semblables :
- le Soleil exerce sur elles une attraction gravitationnelle, qui ressemble à l'attraction de l'aimant sur la bille ;
- lancée sur son orbite, la planète devrait aller tout droit pour satisfaire au principe d'inertie. Mais attirée par le soleil, sa course est infléchie, et elle tourne autour.
Mouvement d'un satellite

A toute petite échelle, on voit la Terre plate. On lance un caillou, il va retomber un peu plus loin en décrivant une belle courbe (une parabole).
A échelle régionale, si on lance une petite fusée, disons avec une vitesse de 5.000 km/h, elle va suivre une même trajectoire, mais plus grande.

La Terre étant courbée, elle retombera beaucoup plus loin. Remarquez les flèches, qui indiquent la direction de la pesanteur : au-dessus, elles semblaient parallèles. Ici, elles ne le sont manifestement plus.

Enfin, si nous lançons maintenant une fusée à plus de 28.000 km/h, elle va aller tellement loin, qu'elle va passer de l'autre côté de la Terre. Et là, elle va encore tomber sur la Terre, mais celle-ci étant toute ronde se dérobe sans cesse ! Ainsi, la fusée n'arrivera plus à retomber sur la Terre, elle va devoir tourner autour... Les flèches indiquant la direction de la pesanteur sont dirigées vers le centre de la Terre.
Un satellite est donc un objet en chute libre, dont le corps attracteur se dérobe sans cesse par sa forme ronde.
Entre la première expérience et la dernière, la forme de la courbe change un peu : d'une parabole, elle passe à une ellipse. Ce changement est dû à la direction de la pesanteur : lorsqu'on peut considérer la pesanteur toujours dans la même direction (premier schéma), le mouvement est une parabole ; lorsque la direction de la pesanteur varie le long de la trajectoire, toujours dirigée vers le centre de la Terre, c'est une ellipse. Mais ce sont deux courbes très proches, on les appelle généralement des coniques. Ce nom générique vient de leur découverte : ellipse, parabole et hyperbole sont les courbes que l'on obtient en coupant un cône par un plan. Le cercle n'est qu'un cas particulier d'ellipse, où l'excentricité est nulle (le plan de coupe est perpendiculaire à l'axe du cône).
La Gravitation Universelle
C'est l'attraction gravitationnelle qui agit sur nous et nous plaque au sol. Autrefois, on ne se posait pas de questions : on imaginait la Terre plate, et il était évident qu'il y avait le haut et le bas. Lorsqu'on a pensé que la Terre pourrait être ronde, on ne comprenait pas comment les Chinois pouvaient marcher la tête en bas !
L'explication est que la Terre attire tout à elle par la gravité. Qu'on soit en France ou aux antipodes, on est attiré vers le centre de la Terre, et le bas est toujours du côté de ce centre, donc du sol. Par analogie, la bille se dirige vers l'aimant, quel que soit le côté où on la lâche.
On dit que la gravité est universelle, parce que c'est une propriété de la matière : tout objet matériel attire tous les autres. La pomme de Newton attire la Terre proportionnellement à sa masse qui est très faible. La Terre attire la pomme proportionnellement à sa masse qui est très grande. Le résultat est que la pomme tombe vers la Terre beaucoup plus que ce que la Terre tombe vers la pomme !
Une autre analogie aide à comprendre : si on se trouve dans une petite barque, et que l'on pousse le quai à l'aide d'un aviron, la petite barque va s'éloigner du quai qui ne bouge pas (presque). Si au lieu de pousser le quai, on pousse une grosse barque, on verra la grosse barque se déplacer un peu !
Reprenons la bille.
Lâchons-la sans vitesse à diverses distances de l'aimant. Elle est attirée plus ou moins fortement : de plus près, la force est plus importante.
Si nous la faisons passer près de l'aimant, elle subira une grande force, et tombera dessus. Pour éviter cela, il faut la lancer plus vite, l'inertie sera alors suffisante pour lui éviter de tomber.
Il en va de même de l'attraction gravitationnelle : le Soleil attire les planètes vers lui, d'autant plus fortement qu'elles sont plus proches. Par conséquent, pour ne pas tomber sur le Soleil, une planète proche doit tourner plus vite qu'une planète lointaine. On peut vérifier cela sur le tableau suivant, qui donne la liste des 9 planètes principales avec leurs caractéristiques orbitales :
| planète | distance (millions de km) | distance (UA) | vitessekm/s | année | inclinaison équateur | inclinaison orbite | excentricité |
| Mercure | 58 | 0,39 | 48 | 88 j | 7° | 7° | 0,21 |
| Vénus | 108 | 0,72 | 35 | 224 j | 3° 4′ | 3° 23′ | 0,01 |
| Terre | 150 | 1 | 30 | 365 j | 23° 26′ | 0° | 0,02 |
| Mars | 228 | 1,52 | 24 | 1 an 321 j | 23° 59′ | 1° 51′ | 0,09 |
| Jupiter | 778 | 5,19 | 13 | 11 ans 314 j | 3° 5′ | 1° 18′ | 0,05 |
| Saturne | 1.430 | 9,53 | 9,6 | 29 ans 167 j | 26° 44′ | 2° 29′ | 0,06 |
| Uranus | 2.876 | 19,2 | 6,8 | 84 ans 7 j | 97° 55′ | 0° 46′ | 0,05 |
| Neptune | 4.506 | 30 | 5,4 | 164 ans 280 j | 28° 48′ | 1° 46′ | 0,01 |
| Pluton | 5.914 | 39,4 | 4,7 | 248 ans 157 j | 122° | 17° 12′ | 0,25 |
Tableau I
Dans ce tableau, UA signifie Unité Astronomique. Nous l'expliquerons plus loin, mais disons simplement que c'est la distance de la Terre au Soleil. Dans cette unité, on voit très facilement que Neptune est 30 fois plus loin du Soleil que nous. Brrr...
Pour la durée de l'année, il faut remarquer que deux phénomènes vont dans le même sens :
- plus on est loin du Soleil, plus la distance à parcourir pour faire un tour est grande. C'est comme pour un coureur de fond qui a davantage de chemin à parcourir quand il est à l'extérieur que quand il est à la corde. A vitesse égale, on mettrait donc plus de temps ;
- mais d'autre part, plus on est loin moins on va vite ! Neptune se déplace presque 10 fois plus lentement que Mercure.
Pour parcourir un chemin beaucoup plus grand à une vitesse plus faible, il faudra beaucoup, beaucoup plus de temps. C'est bien ce que l'on voit aussi sur le tableau.
Le dieu Mercure est toujours représenté avec de petites ailes aux pieds. Il est donc bien choisi pour représenter la championne des planètes !
Quand à Pluton, son nom est placé en italique, parce que l'Union Astronomique Internationale a décidé de la déclasser ! Pluton n'est plus une planète, mais simplement une planète naine parmi de nombreuses conseurs. On verra ceci en temps utile.
Orbites des planètes
Les orbites des planètes sont en général des ellipses, et le Soleil est toujours placé à l'un des foyers de l'ellipse. L'excentricité indique le taux d'aplatissement de l'ellipse. Une excentricité nulle indique un cercle, une excentricité égale à 1 indique une autre conique, qui n'est plus une ellipse, et qui ne se referme pas sur elle-même : c'est une parabole. On remarque que dans le tableau, toutes les excentricités sont comprises entre 0,01 et 0,25. Toutes les planètes ont donc bien des orbites elliptiques, et la plupart sont presque des cercles.
Tracer une ellipse (animation et explications)
Mais on peut donner une appréciation de ces orbites : 0,01 indique une ellipse très proche d'un cercle ; 0,25 est une forte excentricité, indiquant une distance très variable de la planète au Soleil. Mercure et Pluton se particularisent sous cet aspect. Le schéma ci-dessous montre deux ellipses, dont les excentricités sont 0,02 à gauche (la Terre), et 0,25 à droite (Pluton). On y voit la position qu'occupe le soleil par rapport à l'aplatissement. Celui-ci n'est pas très sensible, même dans celle de droite, mais on voit très bien que le soleil est décalé. Il s'ensuit que la distance de la planète au soleil est fortement variable à droite.
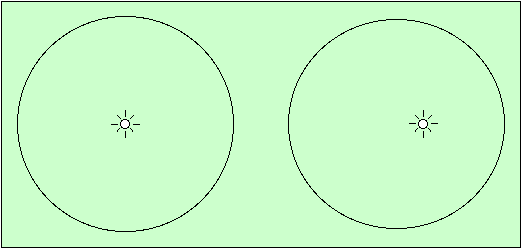
Si la trajectoire d'une planète est une ellipse marquée (forte excentricité), elle se rapproche et s'éloigne du Soleil au cours du temps. Lorsqu'elle est plus proche, elle subit une gravité plus forte, elle doit aller plus vite ; et lorsqu'elle est plus loin, elle ralentit. La vitesse d'une planète sur son orbite est donc constamment variable (dans le tableau précédent, les vitesses indiquées pour les planètes sont les vitesses moyennes ; dans le schéma ci-après, l'excentricité est très exagérée pour mieux illustrer le propos).
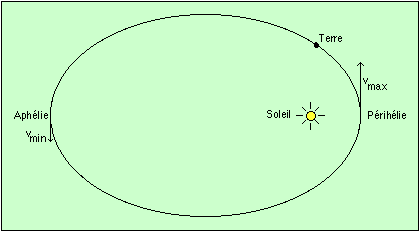
Le schéma montre la Terre sur son orbite (d'excentricité très, très fortement exagérée) autour du Soleil. Le point où elle se trouve le plus près est le périhélie, le point le plus lointain est l'aphélie.
C'est Kepler qui a montré que les planètes se déplacent sur des orbites elliptiques, et qui a découvert les lois du mouvement. Il a analysé les positions de la planète Mars relevées pendant de nombreuses années par Tycho-Brahé. Cette découverte est empirique : il a simplement recherché l'excentricité et le demi grand axe d'une ellipse qui passerait par les points mesurés, sans pouvoir expliquer pourquoi la planète suivrait cette trajectoire. Il n'avait aucune notion de la cause, mais il a su parfaitement formaliser les effets. C'est Newton, un peu plus tard, qui nous donnera la loi de la gravitation universelle. A partir de cette loi, il est aisé de retrouver par le calcul les lois de Kepler (d'autant plus que Newton a utilisé les lois de Képler pour obtenir la gravitation universelle). Donc la loi de Newton explique d'une certaine manière, par une mystérieuse force attractive qui agit instantanément à grande distance, les lois de Kepler.
Cette explication sera jugée insatisfaisante au début du 20ème siècle, et Einstein donnera une nouvelle théorie, la Relativité Générale, qui supprime la notion newtonienne de force, et la remplace par une explication géométrique du mouvement.
Les lois de Kepler
On appelle rayon vecteur la ligne imaginaire qui relie, à tout instant, la planète au Soleil.
1 les planètes se déplacent sur des orbites planes elliptiques, dont le Soleil occupe l'un des foyers
2 le rayon vecteur, reliant la planète au Soleil, balaye des aires égales en des temps égaux (loi des aires)
3 le rapport des cubes des demi grands axes aux carrés des périodes est constant (loi harmonique).a3 / T2 = constante
La loi des aires précise ce que l'on a constaté : en 24 heures, la planète doit se déplacer beaucoup plus au périhélie qu'à l'aphélie pour balayer une même aire.
La loi des aires traduit la conservation de l'énergie.
Dans la troisième loi, a est le demi grand axe de l'orbite, et T la période de révolution (la durée de l'année). La loi indique donc que pour toutes les planètes, le cube du demi grand axe divisé par le carré de la période, donne la même valeur ! Cette loi est extrêmement utile, car il est facile de mesurer la période de révolution d'une planète quelconque. Connaissant cette période, la loi donne le demi grand axe de la planète par simple comparaison avec la Terre (voir calcul de la distance un peu plus bas).
Animation montrant la loi des aires
Le plan de l'orbite terrestre est appelé écliptique, car c'est là que se produisent les éclipses (le Soleil est forcément toujours dans l'écliptique, et les éclipses font intervenir le Soleil).
La troisième loi permet de calculer les distances au Soleil : il est assez facile de mesurer le temps mis par une planète pour faire le tour du Soleil (sa période) ; connaissant la période et la distance de la Terre au Soleil, on en déduit donc celle de la planète au Soleil. En prenant la distance de la Terre au Soleil comme unité (l'unité astronomique) , on peut même connaître les rapports des distances des planètes entre elles, sans connaître la distance de la Terre au Soleil en km. Ce fut longtemps le cas, car cette mesure absolue est assez difficile à faire.
Remarque : la 3ème loi de Képler est approximative ; elle est satisfaite si on considère que les masses des planètes sont négligeables devant celle du Soleil. La théorie de Newton en donne une expression très légèrement différente, plus exacte.
Terminologie
Pour des raisons historiques, lorsqu'un astre tourne autour d'un autre plus massif, le point où les deux astres sont les plus proches, et le point où ils sont les plus éloignés, portent des noms différents selon l'astre central :
| astre central | plus proche | plus lointain |
| le Soleil (Hélios) | périhélie | aphélie |
| la Terre (Gée) | périgée | apogée |
| la Lune (Sélénée) | périsélénée | aposélénée |
| un astre générique (aster) | périastre | apoastre |
Du grec péri = proche, et apo = loin.
Année anomalistique : intervalle de temps qui s'écoule entre deux passages successifs de la Terre à son périhélie.
Année tropique : intervalle de temps qui s'écoule entre deux passages successifs de la Terre au point vernal.
Calcul de la distance
Calculer la distance de Jupiter au Soleil d'après la distance de la Terre au Soleil et la durée de l'année jovienne (facile à mesurer), en utilisant la 3ème loi de Kepler. En parlant de distance, on considère simplement le demi grand axe de l'orbite, qui en donne une bonne idée. On note aT le demi grand axe de la Terre, aJ celui de Jupiter. Et on note TT la période de révolution de la Terre (la durée de l'année), et TJ celle de Jupiter (la durée de l'année jovienne).
Période de Jupiter : TJ = 11 ans et 314 jours ; TT = période de la Terre : 365 jours ; distance de la Terre au Soleil : aT = 1 UA. aJ est donc l'inconnue du problème.
Traduisons d'abord la période de Jupiter en jours pour qu'elle soit comparable à celle de la Terre : TJ = 11 × 365 + 314 = 4.329 jours.
Réponse : on calcule a3 / T2 pour la Terre et pour Jupiter. Pour Jupiter, le résultat dépend de l'inconnue. On écrit ensuite que ces deux valeurs sont égales :

et aJ = 5,2 UA (comparez à la valeur donnée dans le tableau plus haut).
La seule question que l'on peut se poser à ce sujet, c'est comment mesurer la période de révolution de Jupiter. Ceci n'est pas tout à fait évident, parce que le Terre se déplace elle aussi : nous n'observons pas Jupiter depuis un point fixe. Mais le calcul est très simple.
La mesure du temps
La mesure du temps est un problème difficile à résoudre lorsqu'on ne dispose pas de moyens techniques importants. Nous en avons pourtant une notion intuitive plus ou moins bonne. Mais on sait bien que le temps ne passe pas aussi vite lorsqu'on attend que lorsqu'on s'amuse ! Il s'agit là bien sûr du temps subjectif. Scientifiquement, on veut mesurer un temps objectif, mais il n'est pas facile à définir.
Pour mesurer le temps, il faut des repères. Ceux-ci seront soit naturels, soit artificiels. Dans les deux cas, ils sont basés sur des phénomènes périodiques, ou tout au moins réguliers.
Le premier instrument de mesure du temps est la clepshydre, ou horloge à eau. L'écoulement de l'eau, relativement régulier, indiquait l'heure. L'eau a été remplacée par le sable, dans les sabliers, sur le même principe. Plus tard, beaucoup plus tard, on a remplacé un écoulement par un phénomène périodique : le mouvement d'un pendule. Mais un pendule laissé à lui-même s'amorti très vite, à cause des frottements. Pour assurer un garde-temps efficace, il faut lui restituer l'énergie perdue, et ceci se fait grâce au système d'échappement. Ces horloges mécaniques, d'une précision de plus en plus grande, ont permi de mesurer les mouvements des astres. L'horlogerie a eu une importance capitale, car seule la conservation du temps peut permettre, sur un navire en pleine mer, de déterminer la longitude. La création d'horloges de marine précises a sans douté marqué l'apogée de ces mécanismes. Aujourd'hui, les oscillateurs mécaniques sont remplacés par des oscilateurs électriques (quartz piezzo-électrique) ou même atomiques (horloges atomiques).
Pendant très longtemps, le mouvement des astres a été considéré comme parfaitement régulier, et la rotation de la Terre a été prise comme étalon de temps. On en a tiré le temps solaire moyen, qui nous sert tous les jours. Les horloges mécaniques étaient périodiquement recalées sur le temps astronomique.
La notion de jour elle-même, bien qu'évidente pour nous, pose un problème majeur : quand commence une journée ? Diverses réponses ont été données, celle que nous employons maintenant fait commencer le jour à minuit, d'autres le faisaient commencer au lever du Soleil, ou au coucher, ou à midi...
Voici pour le début, mais qu'en est-il de la durée ? Ceci aussi semble naturel, le jour dure 24 heures bien régulières... Mais si vous plantez un bâton vertical dans le sol, et si vous notez à quelle heure de votre montre l'ombre est la plus courte, vous aurez des surprises : ce n'est jamais à la même heure, et c'est rarement à midi ! L'heure que marque un cadran solaire (le bâton est un gnomon, son ancêtre), donne le midi vrai du lieu où l'on se trouve. Complication supplémentaire, mais les voyages en avion nous ont bien habitués au décalage horaire, qui n'est rien d'autre que la constatation du fait qu'il n'est pas midi partout au même moment !
Jour sidéral
Le jour sidéral est l'intervalle de temps qui s'écoule entre deux passages d'une même étoile au méridien. Les étoiles étant à des distances extrêmement grandes, il délimite un tour complet de la Terre sur elle-même.
Jour solaire
Le jour sidéral n'intéresse par grand-monde, à part les astronomes. C'est le jour solaire qui règle notre vie. Le jour solaire vrai est l'intervalle de temps entre deux midis vrais successifs. Puisqu'il est sans cesse variable, il ne serait pas possible de régler une montre sur ce feu follet. Alors, on définit le jour solaire moyen, comme étant la durée moyenne du jour solaire vrai sur une longue période.
Quelle est la différence entre le jour sidéral et le jour solaire moyen ? Supposons que l'orbite de la Terre soit parfaitement circulaire (elle n'en est pas loin) :
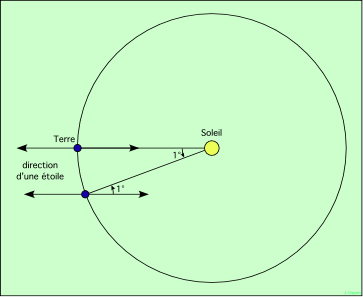
Dans la première position dessinée, le Soleil, la Terre et une étoile sont alignés. Après un tour exactement sur-elle-même, la Terre se retrouve tournée vers la même étoile, mais le Soleil n'est pas au rendez-vous, parce que la Terre s'est déplacée sur son orbite, en lui tournant autour. Pour retrouver le Soleil en face, il lui faut faire encore une petite fraction de tour. L'angle qu'il lui faut faire est égal à l'angle que font ses deux positions successives par rapport au Soleil. Or il est très facile à évaluer : La Terre fait un tour en 365 jours, ce qui est peu différent de 360. Donc, la Terre fait à peu près un degré par jour. Il lui reste donc à faire un degré sur elle-même. Puisqu'elle fait un tour complet (360°) en 24 heures = 24 x 60 x 60 = 86.400 secondes, elle fait un degré en 86.400 / 360 = 240 secondes = 4 minutes. Si on fait le calcul avec 365 jours, on trouve 3 mn 56 s. C'est la différence entre le jour sidéral et le jour solaire moyen. Il est facile de voir que c'est le jour solaire moyen qui est le plus long, donc : jour solaire moyen = jour sidéral + 3 mn 56 s
L'orbite de la Terre n'étant pas vraiment un cercle, le jour solaire vrai est légèrement variable. La différence entre le jour solaire moyen et le jour solaire vrai se nomme équation du temps. Elle est parfois dessinée sur les cadrans solaires.
Basé sur la loi de Newton, le temps des éphémérides est un temps plus théorique, qui est censé être parfaitement régulier. C'est celui des équations.
L'année sidérale
Comme pour repérer le jour, on repère l'année par rapport aux étoiles, c'est l'année sidérale qui vaut 365,25636042 jours solaires moyens. Cette valeur correspond aussi à l'intervalle de temps entre deux passages de la Terre au périhélie.
Mais il y a un problème, c'est celui de la précession des équinoxes. Les saisons ne suivent pas exactement ce rythme, parce qu'elles sont déterminées par le mouvement apparent du Soleil par rapport à l'équateur. Or celui-ci tourne lentement, entraînant l'équinoxe de printemps dans une ronde au ralenti. L'année des saisons se nomme année tropique. On constate qu'elle vaut 365,2422 jours solaires moyens. Elle est donc plus courte que l'année sidérale 365,25636042 - 365,2422 = 0,01416 jour, ou 20 minutes 23 s.
année tropique = année sidérale - 20 mn 23 s
A raison d'un déplacement de 0,01416 jour par an, il faudra 365 / 0,01416 ans pour faire un tour complet, c'est-à-dire 25.000 ans à peu près. C'est la période de la précession. Elle correspond à une avance de 360° / 25.000 = 360 x 60 x 60 / 25.000 = 50" d'arc par an. C'est la valeur de la précession annuelle.
Nous n'entrerons pas ici dans les détails de la mesure du temps. Mais il en est un aspect qui intéresse tout le monde, par son côté pratique de tous les jours, c'est celui qui concerne la mesure des périodes relativement longues, de l'heure à l'année ou au siècle. Ces durées sont un peu plus faciles à apréhender que les plus courtes, et ont été étudiées et maîtrisées avant. Elles donnent lieu à l'établissement d'un calendrier, qui fait l'objet d'une étude à part.
Le Soleil
Bien qu’il nous apparaisse infiniment plus brillant, le Soleil est une étoile. La seule différence est qu’il se trouve très près de nous (à l’échelle astronomique) alors que les étoiles sont beaucoup plus loin. Pour donner un ordre de grandeur, les étoiles les plus proches sont 300.000 fois plus loin que le Soleil ! Pour imaginer la différence, considérez une ampoule de 60 W située à 1 mètre de vous, et une autre identique à 300 km…
La nature du Soleil est restée longtemps incomprise, il fallut attendre le début du XXe siècle pour la comprendre.
La couronne solaire
Au cours d’une éclipse totale de Soleil, on peut d’abord voir le disque noir de la Lune grignoter le Soleil. On peut suivre une éclipse de Soleil sur le sol, sous un arbre. En effet, il y a de petits interstices entre les feuilles qui laissent filtrer un peu de soleil. Par ces petits trous, on obtient une image projetée du Soleil sur le sol. A mesure que la Lune le masque, on voit les petites tâches rondes sous les arbres se transformer en croissants ! Un petit trou par où passe la lumière s’appelle un sténopée.
Petit à petit, la Lune recouvre le Soleil de plus en plus, pour finalement le cacher complètement. A ce moment-là on découvre un spectacle magnifique, et insoupçonné : la couronne. Le Soleil est constitué de plusieurs parties, la plus évidente étant la photosphère, le disque visible. Mais au-delà de la photosphère, le Soleil possède ce qu’il est convenu d’appeler une atmosphère. Celle-ci est encore divisée en plusieurs couches : la plus basse est nommée chromosphère, car elle est de couleur rose. Ce n’est qu’une mince pellicule, qui n’est pas facile à distinguer. Mais la couche au-dessus, la couronne, s’étend très loin du Soleil, et ne possède pas la forme sphérique. Elle est irrégulière, avec des jets plus ou moins importants selon la date à laquelle se produit l’éclipse. Il faut savoir en effet que le Soleil possède un cycle d’activité de 11 ans, et que l’extension de la couronne en dépend.
La brillance de la couronne n’est que le millionième de celle de la photosphère, autant dire que la moindre parcelle de photosphère encore visible suffit à la masquer. Justement, quelques instants avant la totalité, le Soleil est presque tout caché, mais on peut en voir encore de minuscules fragments dans les creux du relief lunaire ! Ces parcelles visibles sont nommées grains de Baily. Le moindre d’entre eux suffit à masquer la couronne.
La brillance de la couronne n’est que le millionième de celle de la photosphère, autant dire que la moindre parcelle de photosphère encore visible suffit à la masquer. Justement, quelques instants avant la totalité, le Soleil est presque tout caché, mais on peut en voir encore de minuscules fragments dans les creux du relief lunaire ! Ces parcelles visibles sont nommées grains de Baily. Le moindre d’entre eux suffit à masquer la couronne.
La photosphère étant beaucoup trop brillante, il n’est possible de voir la couronne que pendant les éclipses totales, qui sont très rares ! Aussi les astronomes se sont longtemps demandé comment faire pour l’observer en dehors de ces instants privilégiés. La réponse a été apportée par Bernard Lyot, qui a réussi à résoudre tous les problèmes d’optique posés. L’instrument s’appelle le coronographe. Grâce à lui, on peut faire des observations de la couronne à tout moment, et l’étude du Soleil a beaucoup avancé.
Cette étude est très importante, car le Soleil est la seule étoile que nous ayons vraiment sous la main ! Toutes les autres sont trop lointaines pour être observées en détail, tout ce que l’on savait d’elles il y a peu de temps encore provenait d’une analyse globale de la lumière qu’elles émettent. On commence seulement maintenant à disposer d’instruments qui donnent quelques détails de la surface des étoiles les plus proches.
L’application des théories physique à l’étude du Soleila permis de construire ce que l’on appelle le modèle standard, qui décrit la composition du Soleil, depuis le centre jusqu’aux plus hautes couches de l’atmosphère, comment se produit l’énergie que le Soleil rayonne, comment elle est propagée depuis le cœur jusqu’à l’espace, etc.
Bien sûr, toutes les étoiles ne sont pas semblables au Soleil,il en est même de très différentes. Mais il est très important de vérifier que toutes les prévisions du modèle standard sont réalisées. Toutes ? Non ! Là aussi une irréductible observation sème la perturbation, alors que tout le reste semble si bien représenter le fonctionnement de notre étoile. Mais ce mal qui répand la terreur, le neutrino puisqu’il faut l’appeler par son nom, était susceptible de remettre en cause soit le modèle standard du Soleil, soit carrément la théorie des particules élémentaires. Mais ceci est une autre histoire…
Les comètes
Les comètes sont des objets éphémères, qui apparaissent un beau jour sans signes précurseurs, évoluent, puis disparaissent. Imprévisibles, elles ont cristallisé toutes les peurs et les superstitions des hommes depuis qu’ils existent. Leur explication correcte est très récente. Leur observation détaillée encore plus : minuscules objets de quelques kilomètre de diamètre, situés à des distances de centaines de millions de kilomètres, elles n’apparaissent que comme de minuscules points faiblement lumineux dans les meilleurs télescopes. Seules les sondes spécialement conçues, envoyées dans leur voisinage (Giotto, Vega, Stardust…) ou même destinées à se poser à leur surface (Rosetta), sont susceptibles de nous donner des renseignements précis.
La mesure des distances
Pour couper une robe, une couturière utilise un mètre en ruban. Mais cette unité n’a plus de sens pour mesurer la distance de Marseille à Grenoble. On utilise alors une unité plus appropriée, le kilomètre. Cet exemple pratique nous montre que pour un même type de mesure, on peut choisir des unités différentes selon l’échelle à laquelle on se place. Il en est de même dans les mesures astronomiques.
Au Moyen-Age, il était difficile d’imaginer ce qu’il y avait au-delà d’une trentaine de kilomètres (sauf pour les pèlerins ou les compagnons). Maintenant, tout le monde a une idée précise de ce qu’est la Terre. La Terre est une petite planète qui tourne autour d’une étoile très quelconque, le Soleil. Entre le Soleil et ses planètes, on peut mesurer les distances en kilomètres. La Terre n’est qu’à 150.000.000 de kilomètres du Soleil, mais Pluton est à 5.900.000.000 de km. Il n’est pas très pratique d’écrire des nombres pareils, et ce qu’on voudrait surtout retenir, c’est que Pluton est beaucoup plus loin que la Terre !
Les astronomes ont défini diverses unités de distance, chacune adaptée à un domaine particulier. Ces distances sont l’unité astronomique, l’année-lumière, le parsec.
Ce n’est pas seulement la difficulté d’écriture des nombres qui a incité les astronomes à définir une unité de distance nouvelle ; c’est bien plus la très grande difficulté de mesurer les distances dans le système solaire directement dans une unité terrestre. Il a fallu attendre des mesures de parallaxe précises, récentes, pour établir le lien entre les distances terrestres et les distances astronomiques. Voyez le principe de la mesure de la distance de Vénus expliqué dans un autre chapitre. Le résultat est une mesure de la distance Vénus-Soleil, en fonction de la distance Terre-Soleil. Donc, si on prend cette dernière comme unité (distance Terre-Soleil = 1), alors la distance Vénus-Soleil est de 0,7.
Les astronomes ont alors pris comme unité la distance de la Terre au Soleil, ils l’ont nommée Unité Astronomique (UA). On peut maintenant dire que la Terre est à 1 UA du Soleil, et Pluton à 5.900.000.000 / 150.000.000 = 39 UA. Le Soleil est 39 fois plus loin que d’ici, il ne doit pas faire très chaud sur Pluton…
On a ensuite mesuré la distance de l’étoile la plus proche de nous : 39.700.000.000.000 km.
Traduisons ce nombre en UA : 39.700.000.000.000 / 150.000.000 = 265.000 UA
C’est encore un nombre bien grand, si on pense que toutes les étoiles sont plus loin que ça, et même beaucoup plus loin.
Mais ce nombre nous apprend déjà que l’étoile la plus proche est tout de même 265.000 fois plus loin de nous que le Soleil !
D’où la définition d’une nouvelle unité plus grande, l’année-lumière : c’est la distance parcourue par la lumière en une année. Pour avoir une idée de ce que cela représente en unités habituelles, convertissons 1 AL en km : la lumière se déplace à 300.000 km/s ; 1 AL = 60 × 60 × 24 × 365 × 300.000 km = 9.460.800.000.000 km ~ 10.000.000.000.000 km = 1013 km = 10.000 milliards de kilomètres… La valeur précise de l’année-lumière est 0,946073047 1013 km, et celle de l’unité astronomique est 149.597.870 km.
Calculer la distance de l’étoile la plus proche de nous en AL : 39.700.000.000.000 / 9.460.800.000.000 = 4,2 AL
L’étoile la plus proche est 8.000 fois plus loin que Neptune.
Pour donner une autre idée des distances, calculons la distance-lumière de Pluton au Soleil : le temps mis par la lumière pour parcourir les 5.900.000.000 km entre le Soleil et Pluton est : 5.900.000.000 km / 300.000 km s-1 = 19.666 secondes = 327 minutes ~ 6 heures. Donc Pluton est à 6 heures-lumière du Soleil, ou bien encore 1/4 de jour, donc 1/4/365 d’année i.e. 0,000 685 AL. C’est moins d’un millième d’année-lumière.
Tout ceci montre que tout est plein de vide !
Représentons le Soleil par une tête d’épingle en verre, d’un millimètre de diamètre. Cette tête d’épingle représente le Soleil de 1,4 million de kilomètres de diamètre. A la même échelle, le diamètre de l’orbite de Pluton est de 4 mètres.
On peut imaginer une tête d’épingle au milieu d’une pièce de 8 mètres de côté (y compris la hauteur du plafond…).
La mesure des températures
La température d’un objet massif, tels que ceux qui nous entourent, est une notion a priori subjective. On a d’abord remarqué que certains matériaux présentaient des variations de volume en fonction de la température : un métal se dilate à la chaleur, et se contracte au froid. Ceci ne constitue pas encore une mesure, car il faut pour cela disposer d’un repère fixe.
La température a été objectivée en 1742 par Anders Celsius, astronome suédois, professeur à l’université d’Uppsala. Il a remarqué qu’un mélange d’eau froide et de glace conservait la même température, même si on l’exposait à un froid plus intense, ou à la chaleur. On peut le constater justement en y plongeant un morceau de métal, dont les variations de longueur dénoteront d’éventuelles variations de température. Tant qu’il reste à la fois de l’eau et de la glace, la température du mélange ne varie pas. On a donc un point fixe.
Pour établir une échelle, il faut de plus un coefficient multiplicateur, la distance entre deux barreaux successifs. Pour cela, un second point fixe est souhaitable. Il a été trouvé par le mélange d’eau et de vapeur, qui conserve lui aussi la même température tant qu’il reste à la fois de l’eau et de la vapeur. Entre ces deux points fixes, Celsius a établit 100 graduations, utilisant donc une division centésimale. La graduation se nomme donc degré Celsius, en référence à son créateur, ou degré centigrade en référence au nombre de divisions.
L’explication de ces deux phénomènes a été trouvée : pour transformer de l’eau en glace, il faut lui retirer de la chaleur ; pour transformer de la glace en eau, il faut lui en fournir la même quantité. Donc, s’il y a à la fois de l’eau et de la glace, lorsqu’on fourni de la chaleur, de la glace l’absorbe pour se transformer en eau, et lorsqu’on retire de la chaleur, de l’eau se transforme en glace. Donc, les variations de température sont absorbées par ces transformations.
Dans le cas de l’eau et de la vapeur, il en est de même. Les variations de température sont gommées.
A l’origine, la température de la glace fondante a été notée 100° et celle de l’eau bouillante 0°. Une permutation de ces deux valeurs a amené l’échelle à celle que nous utilisons tous les jours.
Mais les physiciens ont rencontré un problème. Comme on fait plus blanc que blanc, on peut faire plus froid que froid : il existe des températures négatives. L’échelle Celsius n’a pas de bornes, ni dans les valeurs positives, ni dans les valeurs négatives. Or cette méthode de mesure a été construite en l’absence d’explication de la chaleur. Qu’est ce qui différencie un objet chaud d’un objet froid ?
Il a fallu comprendre que la matière est faite d’atomes, que l’on peut voir ici comme de petites billes, pour arriver à comprendre : la chaleur mesure l’agitation des atomes ! Une particule animée d’une vitesse possède une énergie cinétique. C’est le cas de tous les objets macroscopiques (essayez donc de vous laisser tomber une boîte de petits poi(d)s sur le pied…). Les molécules de l’air (formées de plusieurs atomes) sont animées d’une grande vitesse. Lorsqu’elles viennent heurter notre peau (à 20° C, la vitesse d’une molécule d’oxygène O2 est de 340 m/s = 1220 km/h, la molécule d’azote est légèrement moins lourde, donc légèrement plus rapide), elles nous communiquent leur énergie cinétique. Chacune en apporte très peu, mais elles sont si nombreuses… Alors, l’impression de chaleur que nous ressentons n’est que l’apport d’énergie produit par des milliards de molécules qui viennent nous percuter. Donc, plus les particules vont vite, plus l’objet qu’elles composent est chaud.
Mais qu’arrive-t-il si les molécules qui composent un objet sont immobiles ? Elle ne nous communiquerons plus d’énergie du tout. Il sera donc difficile de faire plus froid ! C’est là la notion de zéro absolu : il existe une température minimale ! Alors qu’il n’existe pas de température maximale, si ce n’est celle qu’aurait un corps dont les atomes iraient à la vitesse de la lumière !!
Des expériences ont montré que cette température est de l’ordre de -273,5° C. On en déduit l’échelle absolue, ou échelle Kelvin (nommée ainsi parce qu’elle a été définie par Lord Kelvin) : le zéro est la température minimum possible, donc approximativement -273,5° C, et les graduations sont les mêmes que dans l’échelle Celsius. Donc le zéro Celsius correspond à 273,5 Kelvins. La conversion est facile :
TK = TC + 273,5
Une température estivale de 26,5° C correspond à 300 Kelvins. La température de la photosphère solaire, qui est de 5.777 Kelvins, vaut donc 5.500° C.
La notion de température que nous avons est basée sur notre immersion dans un environnement de densité élevée. De l’air chaud nous chauffe. Mais que se passe-t-il si on chauffe à 1.000 Kelvins de l’hydrogène à une densité de quelques atomes au cm3 ? Que ressentirait-on si on pouvait exposer sa main à un tel gaz ? Bien que chaque atome percuterait notre peau à très grande vitesse, et y déposerait une énergie importante (à l’échelle de l’atome), ceci ne représenterait pratiquement rien pour nous, et serait strictement insensible (bien que ça pourrait faire des dégats au niveau microscopique).
La chaleur qu’un corps nous communique est due à un grand nombre de chocs à chaque seconde, dans un milieu dense. Dans un milieu très raréfié, même si la température est très élevée, l’apport d’énergie reste très faible sinon négligeable.
Les objets astronomiques
Pour les étoiles, c’est très simple. Elles se forment à partir du milieu interstellaire, qui a été créé juste après le Big Bang. Sa composition comprend à peu près 75 % d’hydrogène et 25 % d’hélium. Ces valeurs sont arrondies, car on ne les connait qu’à quelque chose près, et le milieu interstellaire contient des traces d’éléments légers, essentiellement du lithium, peut-être un peu de bérylium et de bore. Rien d’autre, à l’origine. Plus tard, les étoiles massives ont synthétisé des éléments plus lourds, qui viennent contaminer le milieu pour moins de 2 %.
Les autres objets (planètes, comètes, astéroïdes…) sont formés d’éléments plus lourds. Les éléments les plus légers, ont été éliminés par les conditions physiques (température notamment). Ils sont donc constitués essentiellement d’éléments plus lourds, oxygène, carbone, azote, calcium…. Or ces éléments ont tendance à se combiner, aux températures qui règnent loin des étoiles, pour former des molécules ; aussi, il n’est pas étonnant de trouver une large panoplie du parfait chimiste dans l’Univers.
Les planètes sont formées des composés chimiques les plus simples, oxydes, carbonates, silicates… On trouve également des métaux à l’état natif, c’est-à-dire non combiné. C’est le cas dans les météorites, car ils proviennent du cœur d’une planète détruite, et les conditions physico-chimiques qui régnaient là ne permettaient pas la constitution de molécules. Une petite remarque au sujet des éléments plus lourds que le fer : il ne peuvent pas être synthétisés dans les étoiles, et trouvent leur origine dans des événements violents de l’Univers, comme les explosions d’étoiles.
Mais il y a aussi des matériaux volatils. L’eau est le premier exemple, et le plus répandu. Elle se présente sous trois formes selon la température et la pression : l’eau liquide, la glace et la vapeur. Ce mot de glace a été créé pour la phase froide de l’eau. Mais maintenant, on l’applique à d’autres situations, plus précisément à d’autres éléments chimiques : on connait bien la glace carbonique, qui a des usages industriels importants. C’est du gaz carbonique (CO2) liquéfié, puis gelé. Elle a un aspect blanc, et ressemble beaucoup à la glace d’eau. Mais on peut faire subir le même traitement à d’autres gaz, pas exemple l’azote. Dans des conditions encore plus sévères de température, l’azote se liquéfie et se gèle. On trouve donc de la glace carbonique sur Mars, de la glace d’azote sur Triton. On nomme donc glace tout gaz, ou tout élément volatil, gelé.
Il y a de la glace d’eau partout !
Les étoiles
Les étoiles sont d’autres soleils. Elles se sont formées d’une manière semblable, sont constituées des mêmes matériaux, brillent pour la même raison. Elles nous apparaissent minuscules et pâles parce qu’elles sont beaucoup plus loin que le Soleil. Mais certaines sont beaucoup plus lumineuses et beaucoup plus chaudes.
Dans un instrument, même modeste, on peut en voir des milliers. Il est impossible de donner un nom à chacune. Pour s’y retrouver, les astronomes ont alors établi des catalogues d’étoiles, que nous verrons dans le chapitre qui leur est consacré.
Les pulsars
Toujours en radio, on a observé des objets variables, mais dont la période est extrêmement courte : quelques secondes, puis pour certains beaucoup moins… De tels signaux périodiques ont été attribués à une civilisation extraterrestre ! Jusqu’au jour où on a compris qu’il s’agissait d’une étoile dont la taille avait considérablement diminué, et qui tournait très, très vite sur elle-même. Comme ses signaux étaient pulsants, par association phonétique avec les quasars, on a nommé ces objets pulsars.
On a depuis trouvé encore d’autres curiosités, nommées blazards, magnétars…
La Voie Lactée, ses dimensions, son nombre d’étoiles
La Voie Lactée est cette bande légèrement lumineuse qu’on peut voir l’été lorsqu’on a la chance de disposer d’un beau ciel, sans lumières parasites (loin de toute agglomération). La nature de cette bande laiteuse (d’où le nom et la légende) a été source de débat chez les astronomes : soit il s’agissait de matière gazeuse, soit c’était un rassemblement de très nombreuses étoiles trop éloignées de nous pour être distinguées séparément. C’est cette seconde explication qui est la bonne, bien qu’il y ait également du gaz dans l’espace.
Notre Voie Lactée est donc formée de quelques 150 milliards d’étoiles, et contient aussi des nuages de gaz sombres ou lumineux, des rassemblements d’étoiles de forme quelconque et lâches ou bien nettement sphériques et compacts… Vue depuis la Terre sous la forme d’une bande lumineuse qui fait le tour du ciel, elle a la forme d’un disque aplati.
A l’œil nu, on peut distinguer trois objets qui ont un peu le même aspect : la nébuleuse d’Andromède dans l’hémisphère nord, et les deux nuages de Magellan dans l’hémisphère sud. Ces deux derniers semblent être des lambeaux détachés de la Voie Lactée. En fait, ce sont d’autres Voies Lactées, nous dirons plus exactement d’autres galaxies. Il en est de même de la nébuleuse d’Andromède, qui est de même nature que la Voie Lactée, mais située beaucoup plus loin, à 2,2 millions d’années-lumière. Pour cette raison, on l’appelle maintenant la Grande Galaxie d’Andromède.
Les galaxies
L’histoire des galaxies est récente. Les objets de Messier, petites taches floues dans le ciel, posaient un problème aux astronomes : quelle est leur nature ? Avec les instruments du XIXe siècle, il était impossible de la découvrir. Etaient-ce des nuages de gaz flottant dans l’espace, ou bien de grands rassemblements d’étoiles, trop proches les unes des autres pour être distinguées depuis la Terre ? A cause de leur aspect, on les a toutes appelées nébuleuses. Certaines présentant une structure spiralée ont pris le nom de nébuleuses spirales.
L’Univers était constitué de la Terre, du Soleil et des planètes, disons du système solaire dans son ensemble, et d’étoiles. Au milieu (en apparence) des étoiles se trouvaient les nébuleuses. La question était de savoir si les nébuleuses étaient du gaz à la même distance que les étoiles, ou bien constituées d’étoiles, et alors beaucoup plus loin. En résumé, l’Univers était-il constitué d’un unique ensemble d’étoiles et de nébuleuses, ou bien de plusieurs ensembles d’étoiles, dont certains apparaissaient sous la forme de nébuleuses ?
Enfin, à la mise en service du téléscope Hooker de 2,50 m au Mont Wilson, on a pu résoudre la nébuleuse d’Andromède en étoiles, montrant donc que certaines nébuleuses étaient d’immenses groupes d’étoiles, situés très loin de nous. La Voie Lactée est notre formation d’étoiles, et les nébuleuses spirales sont des formations semblables. On a donné le nom de galaxies à ces formations. La Voie Lactée est souvent notée Galaxie, avec une majuscule. Cette découverte a multiplié par 1.000.000 la dimension de l’Univers, et notre façon de le concevoir.
On a depuis observé des millions de galaxies. Chacune contient une centaine de milliards d’étoiles !
Les étoiles dans une galaxie
Lorsqu’on regarde une belle galaxie comme celle d’Andromède, on a l’impression de voir des étoiles qui se touchent. La réalité est bien différente. Cette illusion est due à l’éloignement et à la perspective. Considérons notre voisinage solaire :
Le diamètre des étoiles est de l’ordre de 106 km (un million de km).Leur distance est de l’ordre de 5 1013 km (1 AL = 10.000 milliards de km).Leur distance est donc 5 1013 / 106 = 5 107 fois plus grande que leur diamètre.
Une tête d’épingle en verre a un diamètre de l’ordre du millimètre. 5 107 fois plus font 5 107 mm = 50 km. On peut donc représenter les étoiles dans une galaxie comme des têtes d’épingles situées à 50 kilomètres les unes des autres !!! On comprend mieux que les collisions d’étoiles soient vraiment exceptionnelles, même dans le cas où deux galaxies se rencontrent.
L’impression que l’on a en regardant une galaxie est donc due à la profondeur : sur la ligne de visée, il y a plusieurs étoiles en perspective, mais éloignées physiquement les unes des autres.
Les amas de galaxies
Les galaxies se groupent à leur tour en amas de galaxies, reliées par la gravité. Les amas en contiennent de quelques centaines à quelques milliers. Ils se regroupent en super amas. L’image que nous avons maintenant de la structure de l’Univers est celle d’une mousse de savon, dans laquelle les parois des bulles sont des amas de galaxies. Nous sommes loin de la Terre au centre de l’Univers !
Ce que nous voyons d’un amas de galaxies représente seulement 1/400e de sa masse ! Où sont passés les 399/400e, nul ne le sait à l’heure actuelle… Et c’est un problème passionnant à résoudre !
Les quasars
Les observations radio ont montré l’existence de sources très intenses, mais dont on ne pouvait pas mesurer la position à cause du faible pouvoir séparateur des instruments. Lorsqu’on a réussi à déterminer précisément la position d’une de ces sources, on a été fort surpris de ne pas trouver d’étoile ou autre objet visible à son emplacement. On a fini par associer la radiosource à une toute petite étoile très faible. Par ses propriétés, cet objet n’était pas une étoile, bien qu’il en ait l’aspect. On l’a alors appelé source radio quasi-stellaire, en anglais quasi-stellar radio source, qui a été contracté en quasar.
Lorsqu’on a réussi à déterminer sa distance à la Terre, la surprise fut grande: elle était très, très loin, et donc dépensait une énergie qu’on ne savait pas expliquer. Ce fut le début d’une longue histoire…
La cosmologie
Après avoir étudié chaque astre séparément, puis par groupement, il sera temps de considérer l’Univers dans son ensemble. C’est le but de la cosmologie (science du cosmos). Elle étudie l’espace (renommé espace-temps) et l’influence de ce qu’il contient (les galaxies étant considérées comme des particules d’épreuve…). De tous temps, l’Homme a cherché à comprendre ce qui l’entoure, depuis les modèles plutôt philosophiques des Anciens, jusqu’aux tentatives scientifiques de la fin du XIXe siècle. Mais il a fallu attendre la théorie de la Relativité Générale pour s’en faire une idée quelque peu acceptable… Cependant, nous ne sommes pas au bout de nos peines, et les interrogations à ce sujet se sont déplacées, mais existent toujours.
Les théories de l’Univers dans son ensemble rejoignent curieusement celles des particules élémentaires chères aux physiciens. Il semble bien difficile d’expliquer l’infiniment grand et l’infiniment petit séparément. Une solution acceptable doit forcément expliquer les deux du même coup!<:p>
Pour cela, il faudra arriver à concilier les deux grandes théories du XXe siècle, la Relativité Générale et la Mécanique Quantique, la première expliquant l’infiniment grand, la seconde l’infiniment petit. L’ennui est que les deux théories s’ignorent, alors que l’Univers est fait de particules…